Задача №112595. Множества и подможества
Рассмотрим множество
A
, содержащее 20 элементов
a
1
, ...,
a
20
., и множество
X
(возможно пустое), являющееся подмножеством множества
A
. От вас требуется по заданному множеству
X
найти все пары множеств
Y
и
Z
(возможно пустые), такие что,
(
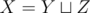Y
и
Z
не пересекаются).
Вам дано описание множества X в виде числа n ( X ) . Если i -ый разряд в двоичной записи n ( X ) равен 1 , элемент a i входит в X . Единственная строка входного файла содержит число 0 ≤ n ( X ) ≤ 2 20 - 1 .
Для каждой пары множеств Y и Z требуется вывести строку, содержащую числа n ( Y ) и n ( Z ) , разделенные пробелом. Числа n ( Y ) и n ( Z ) определяются аналогично числу n ( X ) из описания формата входных данных.
Пары множеств следует выводить в лексикографическом порядке (в порядке возрастания пар чисел n ( Y ) и n ( Z ) ).
11
0 11 1 10 2 9 3 8 8 3 9 2 10 1 11 0