Задача №112879. Японский кроссворд
Маша любит решать японские кроссворды. Так называется головоломка, в которой нужно закрасить некоторые клетки прямоугольника N × M таким образом, чтобы на каждой из N вертикалей и на каждой из M горизонталей количество закрашенных ячеек равнялась некому заранее определенному числу, записанному на полях, для каждой вертикали и горизонтали
К сожалению, иногда составители кроссвордов ошибаются, и кроссворд решения не имеет. Маша не хотела бы тратить время, на решение таких кроссвордов.
Напишите программу, которая для заданных величин N и M , а также N + M чисел, записанных на полях кроссворда, определит, существует ли решение у данного кроссворда.
В первой стоке входного файла записано число T , 1 ≤ T ≤ 6 - количество кроссвордов для проверки. В следующих T × 3 строках идет описание кроссвордов, по три строки на кроссворд. В первой строке заданы два числа N и M , N , M ≤ 10 5 - ширина и высота кроссворда. Во второй строке записаны N целых, неотрицательных чисел - количество закрашенных клеток в каждом из столбцов с первого по N . В третей строке записаны M целых, неотрицательных чисел - количество закрашенных клеток в каждой строчке с первой по M . Ни одно из чисел во второй и третьей строках не превышают общего количества ячеек на соответствующей вертикали или горизонтали.
Выходной файл должен содержать ответ для каждого из кроссвордов в отдельной строке: 1, если кроссворд имеет решение, и 0, если нет. Ответы нужно выводить в том же порядке, в котором во входном файле представлены соответствующие кроссворды.
Тесты состоят из четырех групп.
- Тест 1 из условия, оценивается в 0 баллов.
- Ни один из размеров каждого из кроссвордов не превышает 5. Эта группа оценивается в 15 баллов, при этом баллы начисляются только при прохождении всех тестов группы.
- Ни один из размеров каждого из кроссвордов не превышает 1000, и при этом хотя бы один из размеров каждого из кроссвордов больше 5. Эта группа оценивается в 35 баллов, при этом баллы начисляются только при прохождении всех тестов группы.
- Хотя бы один из размеров, одного из кроссвордов больше 1000. Эта группа оценивается в 50 баллов, при этом баллы начисляются только при прохождении всех тестов группы.
В первом случае кроссворд имеет следующее решение:
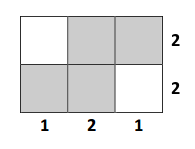 Во втором случае кроссворд неразрешимый: с одной стороны, строка с пятерок показывает, что все вертикали полностью закрашены; с другой стороны, строка из нулей означает, что ни одна из горизонталей не содержит закрашенной клетки. Такого, очевидно, быть не может.
Во втором случае кроссворд неразрешимый: с одной стороны, строка с пятерок показывает, что все вертикали полностью закрашены; с другой стороны, строка из нулей означает, что ни одна из горизонталей не содержит закрашенной клетки. Такого, очевидно, быть не может.
2 3 2 1 2 1 2 2 4 5 5 5 5 5 0 0 0 0 0
1 0