Вам задаётся определенное бинарное дерево поиска, которое по определению удовлетворяет следующим условиям: ключ каждой вершины больше, чем ключ её левого ребёнка и меньше, чем ключ её правого ребёнка.

Кроме того, каждая вершина дерева имеет приоритет, приоритет каждой вершины меньше, чем приоритет её детей.

Известно, что ключи и приоритеты вершин различны. Отсюда получается интересный результат: форма дерева полностью задаётся значениями ключей и приоритетов. Это происходит из-за того, что такое дерево может быть получено как обычное дерево поиска, вершины в которое были добавлены в порядке приоритета.

Глубина вершины – это расстояние от корня до неё, увеличенное на единицу.

Кроме ключа и приоритета, кажная вершина имеет частоту посещения. Мы определяем стоимость посещения вершины как произведение частоты посещения на глубину вершины. Общая стоимость посещения определяется как сумма стоимостей посещения всех вершин дерева.

Для каждой вершины Вам заданы значения ключей, приоритетов и частот посещения. Вы можете изменять приоритеты вершин как Вам хочется, но каждое изменение будет стоит K единиц. Вы можете изменять приоритет любой вершины на любое действительное число, но после изменения все приоритеты должны остаться различными. Ваша цель – минимизировать сумму общей стоимости посещения и общей стоимости изменения приоритетов.

Формат входных данных

Первая строка содержит два числа, \(N\) и \(K\): количество вершин и цену изменения приоритета соответственно. Далее следуют \(N\) чисел: ключи вершин. Далее следуют \(N\) чисел: приоритеты вершин. Далее следуют \(N\) чисел: частоты посещения вершин. Все ключи, приоритеты и частоты посещения не превышают 400000, все числа разделены пробелами.

Формат выходных данных

В нём должно содержаться единственное число: минимальную общую стоимость.

Комментарий к примеру

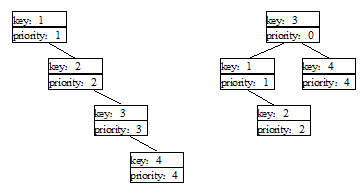
Входное дерево изображено слева. Его общая стоимость посещения: \(1 \times 1+2 \times 2+3 \times 3+4 \times 4=30\). В правильном решении нужно сменить приоритет третьей вершины на 0, получая дерево, изображённое справа. Его общая стоимость посещения: \(1 \times 2+2 \times 3+3 \times 1+4 \times 2=19\)，, стоимость изменения приоритета – 10, итоговая сумма: 29.

Система оценки

• В 40% тестовых примеров выполнено \(N \le 30\).
• В 70%: тестовых примеров выполнено \(N \le 50\).
• В 100%: тестовых примеров выполнено \(N \le 70, 1 \le K \le 30000000.\)

4 10
1 2 3 4
1 2 3 4
1 2 3 4

29