Задача №113315. Клуб веселых и находчивых
Во всех школах и вузах России школьники и студенты любят играть в КВН. А в КВН есть обязательное "домашнее задание", когда вся команда или часть команды участвуют в веселом представлении. В этом году наша любимая команда нашей любимой гимназии решила начать "домашнее задание" тем, что N ребят по росту выстраиваются в шеренгу, размахивая транспарантами и воздушными шариками. Понятно, что в шеренге мальчики и девочки стоят вперемешку - в соответствии со своим ростом. Транспаранты и шарики КВН-щики будут держать в руках и размахивать ими во время представления.
Идея просто отличная, но, к сожалению, транспаранты получились достаточно большими, и капитан команды решил, что "сильный пол должен быть сильным" и, следовательно, каждый такой плакат должны держать два мальчика, которые в шеренге стоят рядом. Две девочки такой плакат не удержат, как, впрочем, и стоящие рядом мальчик и девочка.
И теперь капитана очень интересует один вопрос - сколько существует разных вариантов расстановки в шеренгу мальчиков и девочек, удовлетворяющих следующим условиям:
- Ровно N учеников становится в шеренгу,
- Ровно K плакатов должны держать ребята,
- Если рядом стоят два мальчика, то они должны оба держать плакат, один левой, второй правой рукой.
- Если мальчик стоит в окружении двух мальчиков, то он и левой и правой рукой держит плакаты,
- Если слева (справа) от мальчика стоит девочка, то левой (правой) рукой он плакат не держит,
- Если слева (справа) от мальчика никого нет, то левой (правой) рукой он плакат не держит.
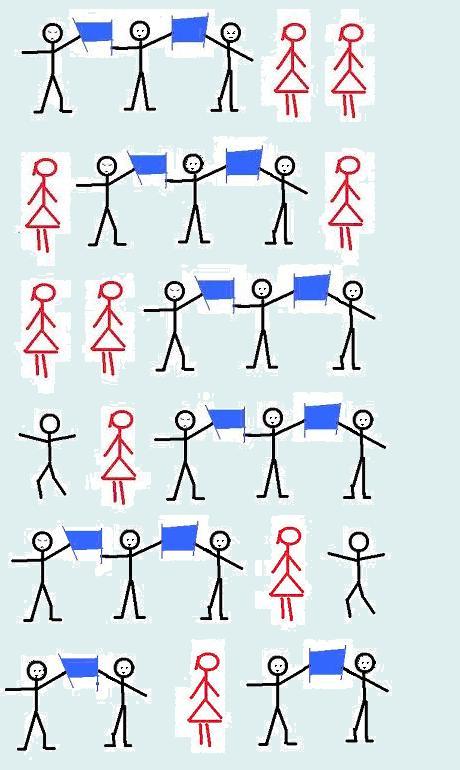
Например, если в шеренгу становятся 5 учеников, которые должны держать 2 транспаранта, то существует 6 вариантов расстановки, которые представлены на рисунке.
Входные данные
Входной файл содержит два целых числа N и K - количество учеников в шеренге и количество транспарантов. Известно, что N и K выбраны таким образом, что результат поместится в 32-разрядной целое число.
Выходные данные
Программа должна вывести одно число - ответ на задачу.
5 2
6
20 8
63426