Задача №113524. Kingdom Plan
Программистам Пете и Гене поручили разработать новый план королевства. Они долго рассуждали и сошлись на мнении, что в идеальном королевстве должно быть ровно N городов и ровно M дорог. Каждая из M дорог должна соединять два различных города, при этом между каждой парой городов может проходить не более одной дороги. Однако между какими именно городами будут проходить дороги, программисты не обсуждали. Они решили, что каждый из них нарисует свою карту дорог идеального королевства, а потом они выберут, чья карта лучше. Начинающий программист Миша, задумался, а стоит ли им вообще выбирать? Может быть, все возможные карты, содержащие N городов и M дорог одинаковые? Миша считает две карты дорог одинаковыми, если можно так пронумеровать города первой карты числами от 1 до N и города второй карты (тоже числами от 1 до N ), что дорога между некоторыми городами в первой карте существует тогда и только тогда, когда существует дорога между соответствующими городами второй карты. Например, карты, показанные на рисунке 1, являются одинаковыми, а на рисунке 2 — различными. По заданным числам N и M определите, могут ли существовать две различные карты дорог.
рисунок 1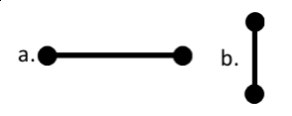 рисунок 2
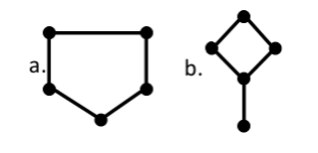
рисунок 2
В первой строке содержатся два целых числа — N и M ( 1 ≤ N ≤ 10 , 0 ≤ M ≤ 45 ). Гарантируется, что существует хотя бы одна карта с N городами и M дорогами.
Если существуют две различные карты дорог, то выведите YES. В противном случае — NO.
Все карты из 2 городов и 1 дороги одинаковые (они соответствуют картам, изображенным на рисунке 1), поэтому не существует двух различных карт и ответ в первом примере NO. На рисунке 2 изображены две различные карты с 5 городами и 5 дорогами, поэтому во втором примере ответ YES.
2 1
NO
5 5
YES