Задача №113705. Крыса - роботяга
Компания « Rapid City Dynamics » знаменита её роботами-собаками, роботами-гепардами и даже человекоподобными роботами. Но большие проекты требуют больших денег, так что компания решила создать что-то простое, но популярное (и более востребованное). Так что компания разрабатывает нового робота « Rat-O-Matic », и вы, как работник « Rapid City Dynamics », принимаете участие в этом.
Робот выглядит как механическая крыса, которая может двигаться и генерировать мелодию, наступая на специальные рамки. Плоскость бесконечна во все стороны, и на ней задана декартова система координат.
Есть ровно n рамок. Каждая рамка задана тремя числами: x , y и r . Она задаёт территорию, ограниченую между двух квадратов со сторонами параллельным осям координат и центрами в точке ( x , y ): радиус первого квадрата r , а второго — 2· r . Радиус квадрата — это расстояние между его центром и стороной. Ко всему прочему, каждой рамке соответствует своя нота. Сейчас есть только 3 возможных ноты, обозначим их как « r », « a » и « t ».
Гарантируется, что никакие две рамки не касаются и не пересекаются.
Вы можете взаимодействовать с роботом, вбивая номер рамки на специальной клавиатуре (рамки пронумерованы начиная с 1 ). Изначально, крыса находится снаружи всех рамок. Благодаря патентованной системе навигации, робот выбирает путь до рамки, который пересекает минимальное количество рамок. Когда крыса наступает на рамку в первый раз, соответствующая нота добавляется в мелодию. Робот останавливается после того, как наступит на нужную рамку.
Известно, что людям нравятся похожие мелодии. В вашей базе данных имеются m мелодий. Каждая мелодия задаётся строкой из символов, которая задаёт ноты. Мелодия, сгенерированная крысой, содержится в мелодии из базы данных, если она содержится в ней в качестве подстроки. Популярность сгенерированной мелодии - это число мелодий в базе данных, которые содержат её. Одинаковые мелодии из базы данных должны быть учтены несколько раз.
В попытке создания самого классного расположения рамок, вы совершили q экспериментов. Эксперименты бывают трёх типов:
- Выключить рамку x . Гарантируется, что рамка была включена до этой операции. Выключенные рамки не влияют на мелодию крысы. Вначале все рамки включены.
- Включить рамку x . Гарантируется, что рамка была выключена до этой операции.
- Посчитать популярность мелодии, сгенерированной роботом при движении от точки с координатами ( 10 9 , 10 9 ) до рамки x . Гарантируется, что рамка x является включённой.
Твоя задача — провести эти эксперименты, используя только свой компьютер!
В первой строке содержится натуральное число n — количество рамок ( 1 ≤ n ≤ 2·10 5 ).
В следующих
n
строках описаны рамки,
i
-я из них содержит три натуральных числа
x
i
,
y
i
,
r
i
и символ
c
i
, разделённые пробелами (
- 10
8
≤
x
i
,
y
i
≤ 10
8
,
1 ≤
r
i
≤ 10
8
, и
c
i
{«
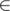r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
Следующая строка содержит натуральное число m — количество мелодий в базе ( 1 ≤ m ≤ 2·10 5 ).
Следующие m строк содержат непустые строки из букв « r », « a » или « t », которые задают мелодии. Суммарная длина всех строк не превосходит 2·10 5 .
Следующая строка содержит натуральное число q — количество экспериментов ( 1 ≤ q ≤ 2·10 5 ).
Следующие q строк описывают эксперименты, j -я из них содержит символ t j (« - », « + » или « ? ») и натуральное число x j отделённое пробелом. Символ задаёт тип эксперимента (« - » — 1, « + » — 2 и « ? » — 3), а число обозначает номер рамки.
Гарантируется, что есть хотя бы один эксперимент третьего типа.
Для каждого эксперимента третьего типа, выведите одно число — популярность получившейся мелодии.
10 баллов — (1 ≤ n, m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 2-6) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 7-9) .
10 баллов — ( 1 ≤ n, q ≤ 100, 1 ≤ m ≤ 200 000 , суммарная длина строк не превосходит 200 000, тесты 10-13) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m ≤ 200 000, 1 ≤ q ≤ 100, суммарная длина строк не превосходит 200 000, тесты 14-16) .
10 баллов — ( 1 ≤ n ≤ 200 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 17-19) .
15 баллов — ( 1 ≤ n, q ≤ 200 000, 1 ≤ m ≤ 100, суммарная длина строк не превосходит 100, тесты 20-23) .
35 баллов — полные ограничения, тесты 24-57.
3 3 3 4 r 2 4 1 a 14 4 1 t 3 rat rara aaa 6 ? 3 ? 2 - 1 ? 2 + 1 ? 2
1 2 3 2