Задача №113888. Бэтмен возвращается
В наши дни Готем Сити состоит из одной улицы, вдоль которой расположены n небоскрёбов. Они пронумерованы с запада на восток числами от 1 до n , при этом i -й небоскрёб имеет высоту h i .
Каждый вечер Бэтмен совершает обзорный полёт над городом. Для этого он забирается на крышу одного из небоскрёбов и планирует с неё на крышу другого небоскрёба. Из-за постоянного сильного ветра он может планировать только в западном направлении, но зато при полёте почти не теряет высоту. Таким образом, он сможет спланировать с небоскрёба номер q на небоскрёб номер p , только если p < q и h p < h q . При этом Бэтмен прекрасно маневрирует в полёте, поэтому высоты и количество небоскрёбов, находящихся между p -м и q -м, значения не имеют. Беспокоясь об уровне преступности в городе, Бэтмен выбирает такие подходящие p и q , что q - p максимально.
Мэрия разработала m планов реконструкции города. Согласно i -му плану будут сохранены только небоскрёбы с l i по r i включительно, а остальные будут снесены. Бэтмен не любит неопределённость, поэтому для каждого плана реконструкции он хочет заранее знать оптимальный способ патрулирования оставшейся части города, то есть такие p i и q i , что l i ≤ p i < q i ≤ r i , h p i < h q i и q i - p i максимально.
В первой строке записано число n ( 1 ≤ n ≤ 200 000 ) — количество небоскрёбов, расположенных вдоль улицы.
Во второй строке записаны n чисел h i ( 1 ≤ h i ≤ 200 000 ) — высоты небоскрёбов, перечисленные с запада на восток.
В третьей строке записано число m ( 1 ≤ m ≤ 200 000 ) — количество планов реконструкции города.
В каждой из следующих m строк записаны по два числа l i и r i ( 1 ≤ l i < r i ≤ n ), которые означают, что в i -м плане мэрия планирует оставить только небоскрёбы с номерами с l i по r i включительно.
Для каждого плана реконструкции выведите два числа — оптимальные p i и q i . Если патрулирование становится невозможным, то выведите -1 -1 .
Если подходящих оптимальных пар небоскрёбов несколько, то выведите любую из них.
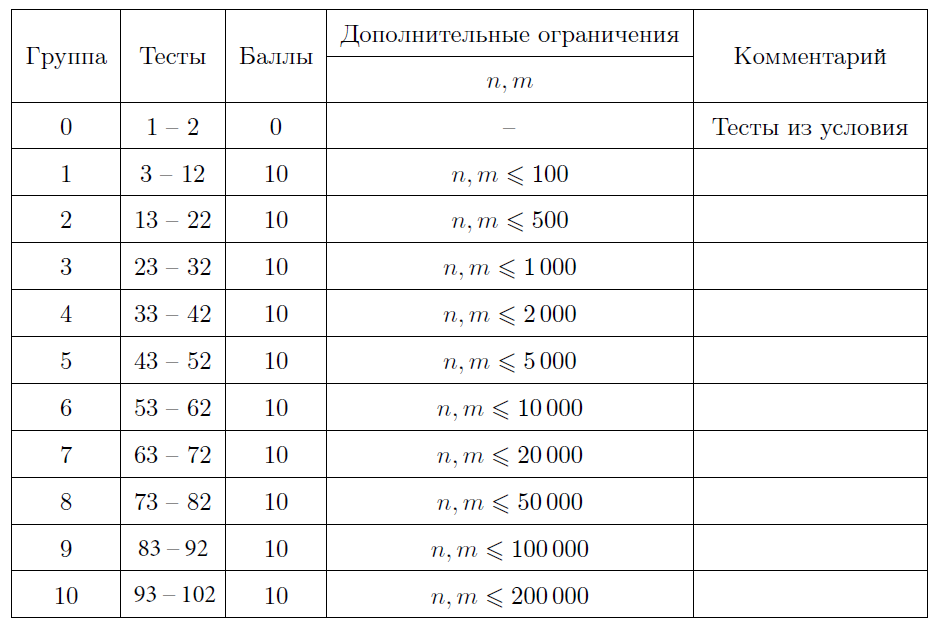
Тесты к этой задаче состоят из одиннадцати групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
Рассмотрим первый тест из условия. В первом запросе единственная доступная пара небоскрёбов имеет высоты 3 и 1 , но она не удовлетворяет условию задачи, так как 3 ≥ 1 . Во втором запросе подходит пара из первого и второго небоскрёбов, так как они имеют высоты 2 и 3 . Рассмотрим второй тест из условия. В первом запросе подходят пары небоскрёбов с высотами 2 и 3 , а также с высотами 2 и 4 . Первая из этих пар находится на большем расстоянии, поэтому именно она является правильным ответом.
4 2 3 1 4 2 2 3 1 3
-1 -1 1 2
7 5 4 2 4 3 1 5 4 2 6 2 7 1 7 3 7
3 5 2 7 2 7 3 7