Задача №113892. Хранители
Хранители в опасности, и Доктор Манхэттен со своим другом Дэниелом Драйбергом должны срочно их предупредить. Всего в команде хранителей n человек, i -й из которых находится в точке плоскости с координатами ( x i , y i ) .
Как всем известно, доктор Манхэттен вычисляет расстояние между двумя хранителями
i
и
j
по формуле
|
x
i
-
x
j
| + |
y
i
-
y
j
|
. Дэниел, как обычный человек, считает, что расстояние равно
 .
.
Сейчас успех операции зависит от того, сколько существует пар ( i , j ) ( 1 ≤ i < j ≤ n ), таких что расстояние между хранителем i и хранителем j , вычисленное Доктором Манхэттеном, равняется расстоянию между ними, вычисленному Дэниелом. Вычислить эту величину попросили именно вас.
В первой строке входных данных записано число n ( 1 ≤ n ≤ 200 000 ) — количество хранителей.
В каждой из следующих n строк записаны два целых числа x i и y i ( | x i |, | y i | ≤ 10 9 ).
Выведите количество пар хранителей, таких что расстояние между ними, вычисленное доктором Манхэттеном, равно расстоянию, вычисленному Дэниелом.
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

В первом примере расстояние между хранителем
1
и хранителем
2
равняется
|1 - 7| + |1 - 5| = 10
в понимании Доктора Манхэттена и
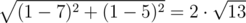 в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
3 1 1 7 5 1 5
2
6 0 0 0 1 0 2 -1 1 0 1 1 1
11