Задача №113899. Открытая олимпиада по дизайну
Если вы вдруг не знаете, то в подготовке соревнований по программированию обычно участвуют люди, которые в прошлом сами являлись участниками подобных соревнований. Это очень удобно: бывшие олимпиадники-программисты часто разбираются не только в написании программ, но и в вёрстке условий, и в настройке тестирующей системы, и ещё в множестве разных интересных (и не очень) дел. А что если бы олимпиаду готовили, например, дизайнеры?
В одной воображаемой вселенной проходит Открытая Олимпиада школьников по Дизайну, состоящая из n задач, которую готовят n дизайнеров условий, один дизайнер названий и один дизайнер шрифтов. Каждый из n дизайнеров условий уже сверстал условие своей задачи, но, так как дизайнеры люди творческие и работают поодиночке, каждый из них оставил разное количество места под название задачи. А именно, макет i -й задачи предполагает l i букв в названии задачи.
Согласно регламенту олимпиады, требуется, чтобы названия задач состояли из символов Юникода, были различны и шли в лексикографическом порядке (см. замечание). Дизайнер шрифтов договорился с дизайнером названий, чтобы тот подобрал такие названия для задач, которые используют как можно меньше различных букв, и дизайнеру шрифтов пришлось бы работать над меньшим количеством изображений символов.
Пока дизайнер названий придумывает названия, дизайнер шрифтов решил поинтересоваться у вас, какое минимальное количество различных букв ему придётся нарисовать, чтобы из них можно было составить различные названия для всех задач и чтобы они шли в лексикографическом порядке. Считайте, что символов в Юникоде достаточно большое количество, чтобы это всегда можно было сделать для любых входных данных, удовлетворяющих ограничениям задачи. Обратите внимание, не разрешается менять порядок задач.
В первой строке входных данных находится целое число n ( 1 ≤ n ≤ 100 000 ) — количество задач в олимпиаде.
Во второй строке находится последовательность целых чисел l 1 , l 2 , ..., l n ( 1 ≤ l i ≤ 10 9 ) — длины названий задач.
Выведите единственное целое число — минимальное количество различных символов, которое потребуется использовать для составления названий для всех задач.
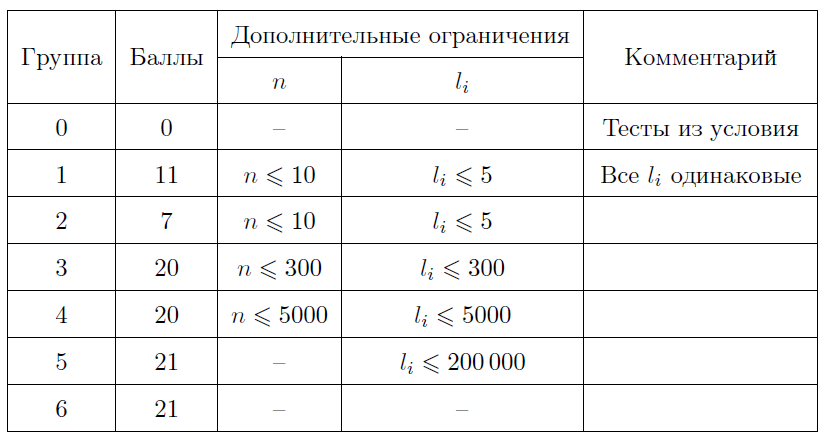
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп кроме тестов из условия. В данной задаче решение не обязано проходить тесты из условия, чтобы быть принятым на проверку.
Строка x 1 x 2 ... x a длины a лексикографически меньше строки y 1 y 2 ... y b длины b , если выполнено одно из двух условий:
- либо в первой позиции i , такой что x i ≠ y i , в первой строке стоит меньший символ, чем во второй, то есть x 1 = y 1 , x 2 = y 2 , ..., x i - 1 = y i - 1 , x i < y i ;
- либо первая строка является строгим префиксом второй строки, то есть a < b и x 1 = y 1 , x 2 = y 2 , ..., x a = y a .
Последовательность различных слов называется упорядоченной лексикографически, если каждое слово в последовательности (кроме последнего) лексикографически меньше следующего слова.
В первом тесте из условия для составления названий задач можно воспользоваться символами « a » < « o » < « x » и составить названия « aa », « ao », « ax », « ox », « xx ».
Во втором тесте из условия можно воспользоваться двумя символами « l » < « o » и составить названия « lol », « o », « ol » и « oo ».
5 2 2 2 2 2
3
4 3 1 2 2
2