Задача №113901. Застройка мегаполиса
В 20 yy году Москва оказалась застроена до такой степени, что в черте города совсем не осталось территории, пригодной для постройки новых зданий. В поисках новых источников дохода правительство города приняло план, согласно которому все железнодорожные пути в черте города реконструируются и заменяются на подземные, а высвобожденная поверхность используется для коммерческой аренды.
Планирование будущей застройки было начато с участка Октябрьской железной дороги длиной в k метров. Так как строить здания поверх образованного туннеля — долгий и сложный процесс, было принято решение закрепить новый участок за наиболее популярными передвижными точками общепита, продающими мороженное, хот-доги, кофе и тому подобное.
Участок для строительства разделён на k сегментов одинаковой длины, последовательно пронумерованных целыми числами от 1 до k . Из n поступивших в правительство заявок на получение территории i -я претендует на сегменты с l i по r i , причём соответствующая точка общепита будет оказывать давление величиной p i на соответствующий отрезок поверхности. Каждую заявку правительство либо отклонит, либо полностью удовлетворит, предоставив точке все запрошенные сегменты.
Правительство города заинтересовано в том, чтобы сдать каждый сегмент новообразованной территории в аренду хотя бы одной точке общепита. При этом, чтобы уменьшить риск обвала туннеля, было принято решение минимизировать максимальное из оказываемых давлений на каком-либо из сегментов. Обратите внимание, что не запрещается сдавать в аренду один сегмент сразу нескольким точкам общепита, но в таком случае давление, оказываемое ими на данный сегмент поверхности, суммируется.
Помогите правительству одобрить такой набор заявок, чтобы каждый сегмент был сдан в аренду хотя бы одной передвижной точке, но максимальное давление, оказываемое на туннель, было как можно меньше.
В первой строке входных данных находятся два целых числа n и k ( 1 ≤ n ≤ 100 000 , 1 ≤ k ≤ 10 9 ) — количество заявок на открытие точек общепита и количество сегментов поверхности.
В последующих n строках описаны заявки, каждая из которых задаётся тремя целыми числами l i , r i , p i ( 1 ≤ l i ≤ r i ≤ 10 9 , 1 ≤ p i ≤ 10 9 ), соответственно границами предприятия и давлением, которое оно оказывает на поверхность туннеля.
Выведите наименьшее возможное максимальное давление, оказываемое на поверхность туннеля точками общественного питания, при условии, что все сегменты поверхности туннеля сданы в аренду. Если не существует способа покрыть весь участок, выведите - 1 .
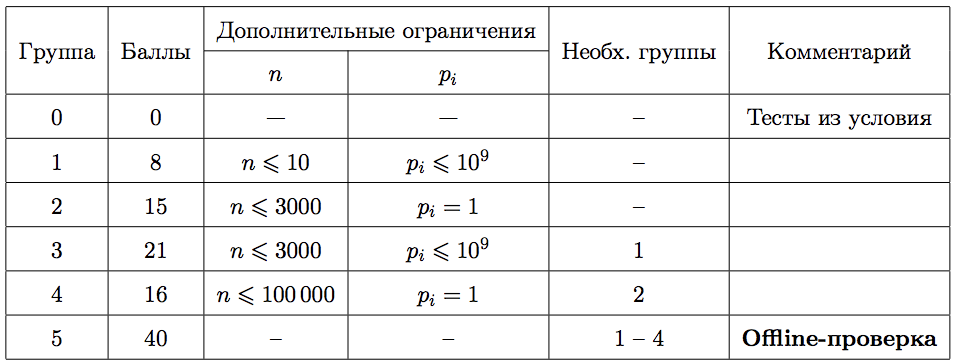
Тесты к этой задаче состоят из шести групп. Баллы за группу ставятся только при прохождении всех тестов группы и всех групп, от которых зависит данная группа (см. таблицу с системой оценивания). Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования. В данной задаче решение не обязано проходить тесты из условия, чтобы быть принятым на проверку.
В первом тесте из условия оптимальное решение — принять первые две заявки, тогда максимальное давление, равное 3 , будет достигаться на третьем сегменте.
Во втором тесте из условия невозможно сдать в аренду третий сегмент.
В третьем тесте из условия одним из оптимальных решений будет удовлетворить все заявки, тогда максимальное давление, равное 8, будет достигаться на четвёртом сегменте. Обратите внимание, что минимизировать или максимизировать количество удовлетворённых заявок не требуется.
В четвёртом тесте из условия оптимальное решение — удовлетворить первую и четвёртую заявки, тогда на все сегменты будет оказываться одинаковое давление, равное 1.
3 4 1 3 1 3 4 2 1 4 5
3
1 3 1 2 1
-1
4 5 1 4 3 4 5 5 1 1 3 1 2 1
8
4 5 1 4 1 4 5 1 3 4 1 5 5 1
1