Задача №113905. Отбой
Преподаватели Летней Какой-нибудь Школы укладывают учащихся спать.
Домик состоит из n комнат, в каждой из которых должны жить ровно b школьников. Однако к моменту отбоя оказалось, что далеко не каждый школьник находится в своей комнате. Комнаты расположены в ряд и пронумерованы по порядку от 1 до n , изначально в i -й комнате находятся a i школьников. При этом, в домике находятся все проживающие в нём школьники и только они, то есть, a 1 + a 2 + ... + a n = nb . В домике также живут p преподавателей, причём p ≤ 2 .
Процесс укладывания школьников спать устроен следующим образом. Один преподаватель встаёт у комнаты 1 и движется в направлении комнаты n . Если есть второй преподаватель, то он встаёт у комнаты n и движется в сторону комнаты 1 . Закончив укладывать очередную комнату, преподаватель переходит к следующей, причём если преподавателей двое, то они входят и выходят из своих комнат одновременно. Если n нечётно, а преподавателей двое, то среднюю комнату укладывает спать только первый преподаватель. Как только все школьники уложены спать, процесс заканчивается.
Когда преподаватель заходит в комнату, он считает количество школьников внутри, затем тушит свет и закрывает комнату. Дополнительно, если количество школьников внутри не совпадает с b , этот преподаватель записывает номер комнаты в свою записную книжку и всё равно тушит свет и закрывает комнату. Преподаватели очень торопятся составить учебный план на завтра, поэтому игнорируют, кто именно находится в комнате, считая только количество школьников.
Пока преподаватели находятся в комнатах, школьники могут перебегать между ещё не закрытыми и не укладываемыми прямо сейчас комнатами, причём школьник успевает перебежать не более чем на d комнат (то есть, перемещается в комнату с номером, который отличается не более чем на d ). Также, после (или вместо) перемещения любой школьник может спрятаться под кровать в той комнате, в которой находится, тогда преподаватель его не заметит при подсчёте. В любой комнате под кроватями могут спрятаться сколько угодно школьников одновременно.
Формально говоря, происходит следующий процесс:
- Объявляется отбой, к этому моменту в комнате i находится a i школьников.
- Каждый школьник может переместиться в другую комнату, но не далее, чем на d от изначального положения, либо остаться в текущей комнате. После этого желающие спрятаться под кровать прячутся.
- В комнату 1 заходит преподаватель (а также в комнату n , если преподавателей двое), укладывает спать всех находящимся там школьников и запирает комнату (после этого нельзя ни войти в комнату, ни выйти из неё).
- Школьники из комнат с номерами от 2 до n (или до n - 1 , если преподавателей двое) могут переместиться в другие комнаты, убегая не далее, чем на d комнат от своего текущего местоположения, либо остаться в текущей комнате. Желающие спрятаться под кровать прячутся.
- Из комнаты 1 в комнату 2 (и, возможно, из комнаты n в комнату n - 1 ) переходит преподаватель.
- Процесс продолжается, пока во всех комнатах школьники не будут уложены спать.
Обозначим за x i количество комнат с видимым нарушением численности, которые были записаны i -м преподавателем. Школьники знают, что директор смены будет слушать жалобы на безобразие во время отбоя не более, чем от одного преподавателя домика, поэтому хотят действовать таким образом, чтобы максимальное из чисел x i было как можно меньше. Помогите им определить, какое минимальное значение эта величина может принимать при оптимальных действиях школьников.
В первой строке записаны четыре целых числа p , n , d и b ( 1 ≤ p ≤ 2 , 2 ≤ n ≤ 100 000 , 1 ≤ d ≤ n - 1 , 1 ≤ b ≤ 10 000 ) — количество преподавателей, количество комнат в домике, максимальное количество комнат, которые успевает пробежать школьник, пока преподавателя нет в коридоре, и требуемое количество школьников в одной комнате.
Во второй находятся n целых чисел a 1 , a 2 , ..., a n ( 0 ≤ a i ≤ 10 9 ), i -е из которых соответствует количеству школьников в i -й комнате перед объявлением отбоя.
Гарантируется, что a 1 + a 2 + ... + a n = nb .
Выведите одно число — минимальное возможное значение максимального x i .
В первом примере школьники достаточно быстро бегают, чтобы разбежаться по своим комнатам ещё до того, как преподаватель войдёт в первую, тем самым ответ 0 .
Во втором примере преподаватель запишет минимум одну комнату в свою записную книжку. Одной из оптимальных стратегий является следующая: перед тем, как преподаватель войдёт в первую комнату, из пятой комнаты по 10 школьников должны перебежать в комнаты 2 , 3 и 4 . Далее в комнатах 2 , 3 , 4 по одному школьнику прячется под кровать, в комнате 5 под кровать прячутся два школьника, после чего школьники не производят никаких действий. При такой последовательности действий школьников преподаватель занесёт в записную книжку только комнату 1 .
В третьем примере первые три комнаты посетит первый преподаватель, а последние две — второй. Одним из оптимальных решений является следующее: на первом шаге три школьника должны перебежать из комнаты 5 в комнату 4 , на втором шаге два из них должны перебежать в комнату 3 и одному из них следует там спрятаться. Тем самым недовольство первого преподавателя вызовет только комната 2 , а второй преподаватель и вовсе не встретит никаких нарушений.
В четвёртом примере одной из оптимальных стратегий является следующая: на первом шаге все школьники из первой комнаты прячутся, а все школьники из второй комнаты перебегают в третью. На втором шаге один школьник перебегает из третьей комнаты в четвёртую, а ещё 5 прячутся. Тем самым первый преподаватель будет недоволен комнатами 1 и 2 , а второй — комнатами 5 и 6 .
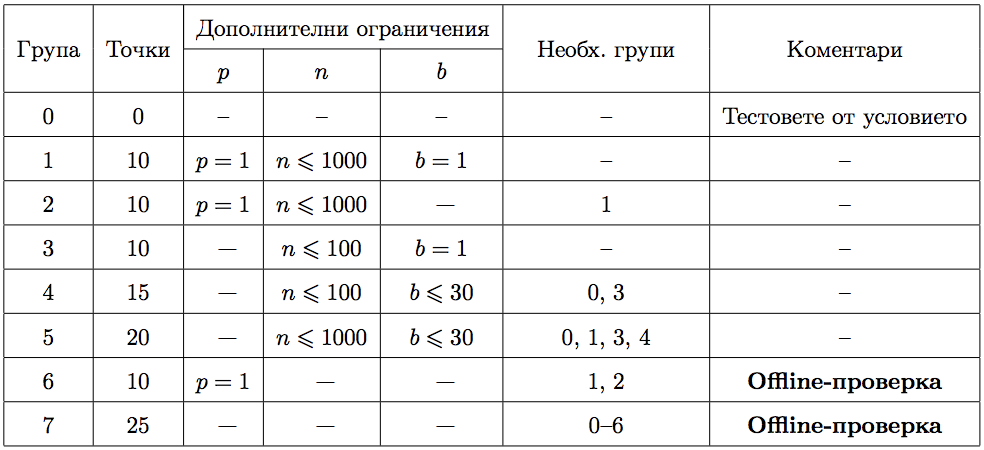
Тесты к этой задаче состоят из семи групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для принятия на проверку. Offline -проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
1 5 3 1 0 0 0 5 0
0
1 5 3 10 5 1 1 1 42
1
2 5 1 1 1 0 0 0 4
1
2 6 1 2 3 8 0 1 0 0
2