Задача №113906. Двоичные карты
Никогда не поздно научиться играть в увлекательную игру под названием «Двоичные карты»!
В игре участвует неограниченное число игральных карт разных положительных и отрицательных достоинств. Абсолютная величина, написанная на любой карте, является степенью двойки, то есть на карте может быть написано либо 2 k , либо - 2 k для некоторого целого k ≥ 0 . Карты любого достоинства имеются в неограниченном количестве.
В начале игрок выбирает себе колоду — некоторое множество (возможно пустое) игральных карт. При этом в колоду разрешается включить произвольное количество карт каждого из достоинств, но уровень игрока оценивают по тому, насколько мало карт он включает в свою колоду. Игра состоит из n конов. На i -м кону жюри называет игроку целое число a i . После этого игрок обязан выложить на стол такое подмножество карт из своей колоды, что сумма достоинств этих карт в точности равна a i (можно не выкладывать никакие карты вообще, тогда сумма считается равной нулю). Если игрок не может выложить нужный набор карт, он считается проигравшим, а игра заканчивается. В противном случае игрок возвращает выложенные карты назад в свою колоду и переходит к следующему кону. Игрок считается победителем, если он на каждом кону смог выложить необходимые карты.
До вас дошли слухи, какие числа a i жюри собирается назвать на каждом кону. Теперь вы хотите выбрать колоду с минимальным количеством карт, которая позволит вам выиграть в «Двоичные карты».
В первой строке находится целое число n ( 1 ≤ n ≤ 100 000 ) — количество названных чисел в игре.
Во второй строке находятся n целых чисел a 1 , a 2 , ..., a n ( - 100 000 ≤ a i ≤ 100 000 ) — числа, называемые на каждом кону.
В первой строке выведите число k ( 0 ≤ k ≤ 100 000 ) — минимальное количество карт, которые нужно выбрать в колоду, чтобы выиграть в «Двоичные карты».
Во второй строке выведите k целых чисел b 1 , b 2 , ..., b k ( - 2 20 ≤ b i ≤ 2 20 , | b i | является степенью двойки) — достоинства карт, составляющих колоду. Достоинства можно выводить в любом порядке. Если существует несколько колод оптимального размера, разрешается вывести любую из них.
Гарантируется, что существует колода карт минимального размера, удовлетворяющая требованиям на величины чисел выше.
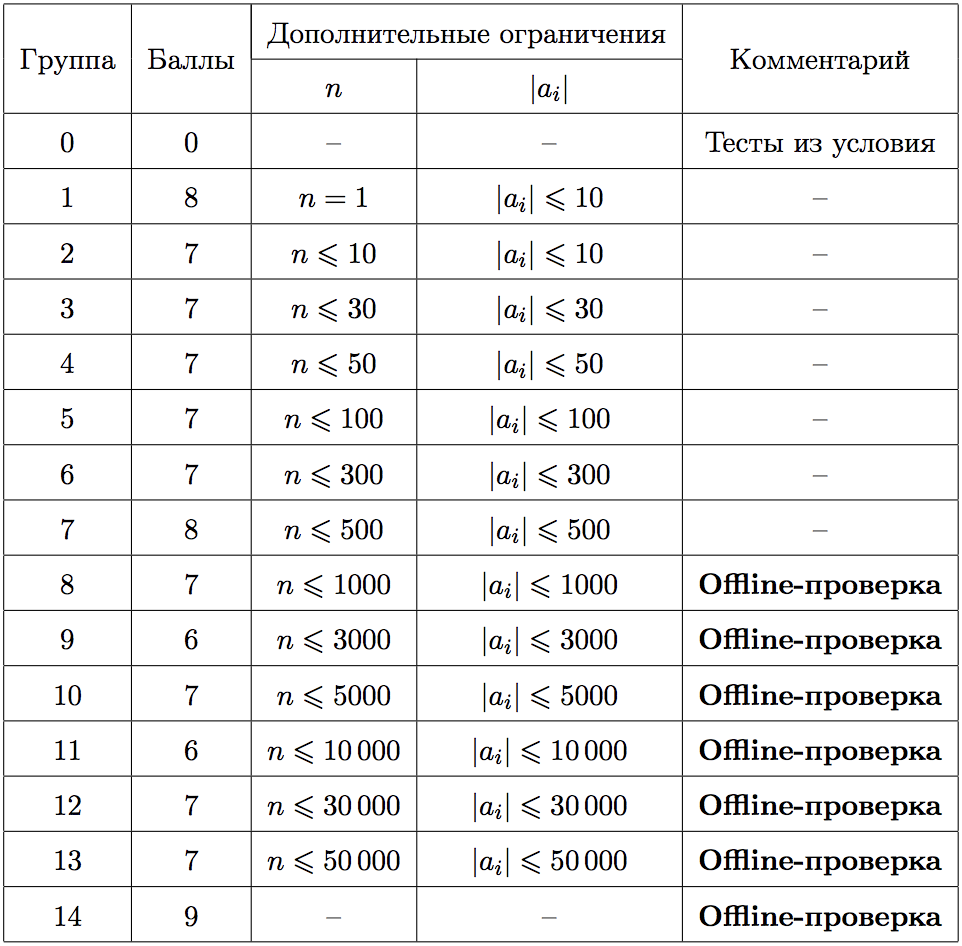
Тесты к этой задаче состоят из четырнадцати групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов всех предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для принятия на проверку. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
В первом тесте из условия на единственном кону можно положить обе карты из колоды. Обратите внимание, этот тест из условия — единственный из подходящих под ограничения первой группы тестов.
Во втором тесте из условия в первый кон можно выложить единственную карту - 1 , во второй кон — карты 4 и - 1 , в третий кон можно не выкладывать ничего, в четвёртый кон — только карту 4 , а в пятый кон — всю колоду.
1 9
2 1 8
5 -1 3 0 4 7
3 -1 -4 8
4 2 -2 14 18
3 -2 4 16