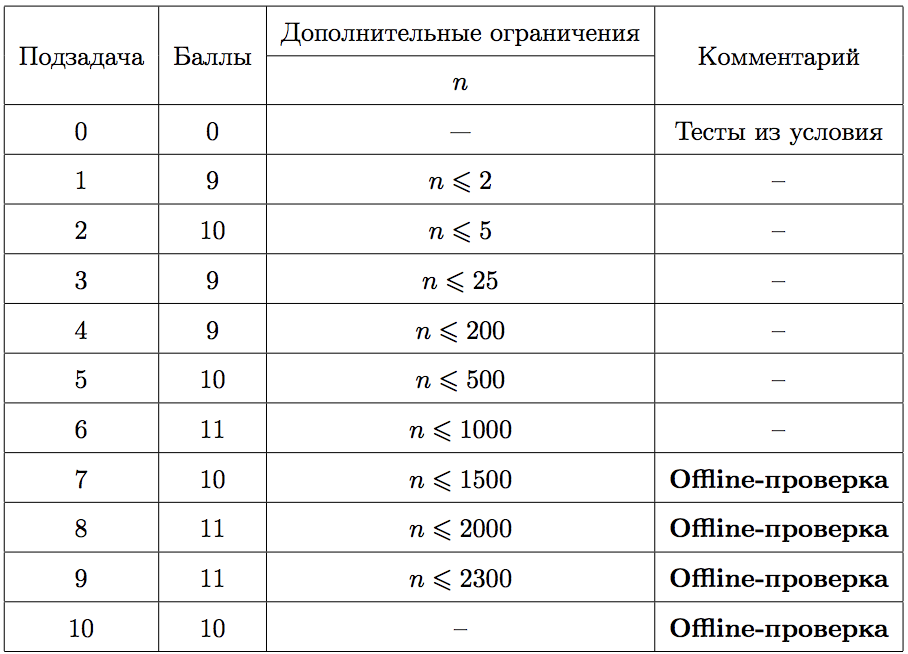
Задача №113908. Астрономия
18 год нашей эры. Известный астроном Филон Берляндский публикует трактат «Об устройстве небесного свода», в котором рассказывает о невероятном явлении, замеченном им во время наблюдений за звёздами. Однажды ночью Филон увидел на безоблачном небе 2 n звёзд и Луну. Удивительно, что звёзды можно было мысленно разбить на пары так, что любая прямая, проходящая через центры двух звёзд из пары проходила также и через центр Луны, при этом все такие прямые были различны. Филон тщательно запечатлел данное явление на карте звёздного неба, в которой была введена система координат, и обнаружил, что центры всех звёзд и центр Луны оказались в точках с целочисленными координатами. Поскольку Филон считал, что Земля и Луна плоские, система координат на карте была двумерная. Система координат была выбрана астрономом так, чтобы координаты всех объектов, включая Луну, по модулю не превосходили 10 6 . Помимо этого, никакие два объекта (две звезды или звезда и Луна) не были в одной точке.
Помимо карты звёздного неба Филон Берляндский написал в своём трактате предсказание, что спустя 2000 лет звёзды на небе вернутся в то же положение, а на месте Луны появится огромная комета, которая уничтожит Землю.
2018 год нашей эры. Вам в руки попадает трактат Филона Берляндского, и вы с ужасом обнаруживаете, что звёзды на небе находятся в том же положении, что и 2000 лет назад! К сожалению, время не пощадило карту астронома, поэтому на ней остались отмеченными только точки, соответствующие центрам звёзд, и не осталось никаких упоминаний, каким образом следовало разбить точки на пары, чтобы все построенные по этим парам прямые прошли через центр Луны. Что ещё хуже, на карте стёрлась точка, соответствующая центру Луны. Чтобы узнать, откуда прилетит комета, и спасти человечество от неминуемой гибели, необходимо срочно восстановить какую-нибудь подходящую позицию центра Луны!
В первой строке задано целое число n ( 2 ≤ n ≤ 2600 ) — количество пар звёзд, которые астроном увидел на небе.
В следующих 2 n строках содержатся пары целых чисел x i , y i ( - 10 6 ≤ x i , y i ≤ 10 6 ) — координаты центров звёзд на карте. Обратите внимание, что звёзды указаны в произвольном порядке, никак не связанном с тем, как Филон Берляндский разделял их на пары. Центры никаких двух звёзд не находятся в одной точке.
Если астроном ошибся, и не существует способа разбить все точки на пары таким образом, чтобы все построенные по этим прямые были различны и пересекались в одной точке с целыми координатами, отличной от центров всех звёзд, то выведите « No » (без кавычек) в единственной строке вывода.
В противном случае в первой строке выведите « Yes » (без кавычек). Во второй строке выведите пару целых чисел x , y ( | x |, | y | ≤ 10 6 ) — координаты точки, в которой находился центр Луны в вашем решении. Если подходящих точек несколько, то выведите любую из них. Обратите внимание, что выведенная точка не может совпадать с центром ни одной из звёзд.
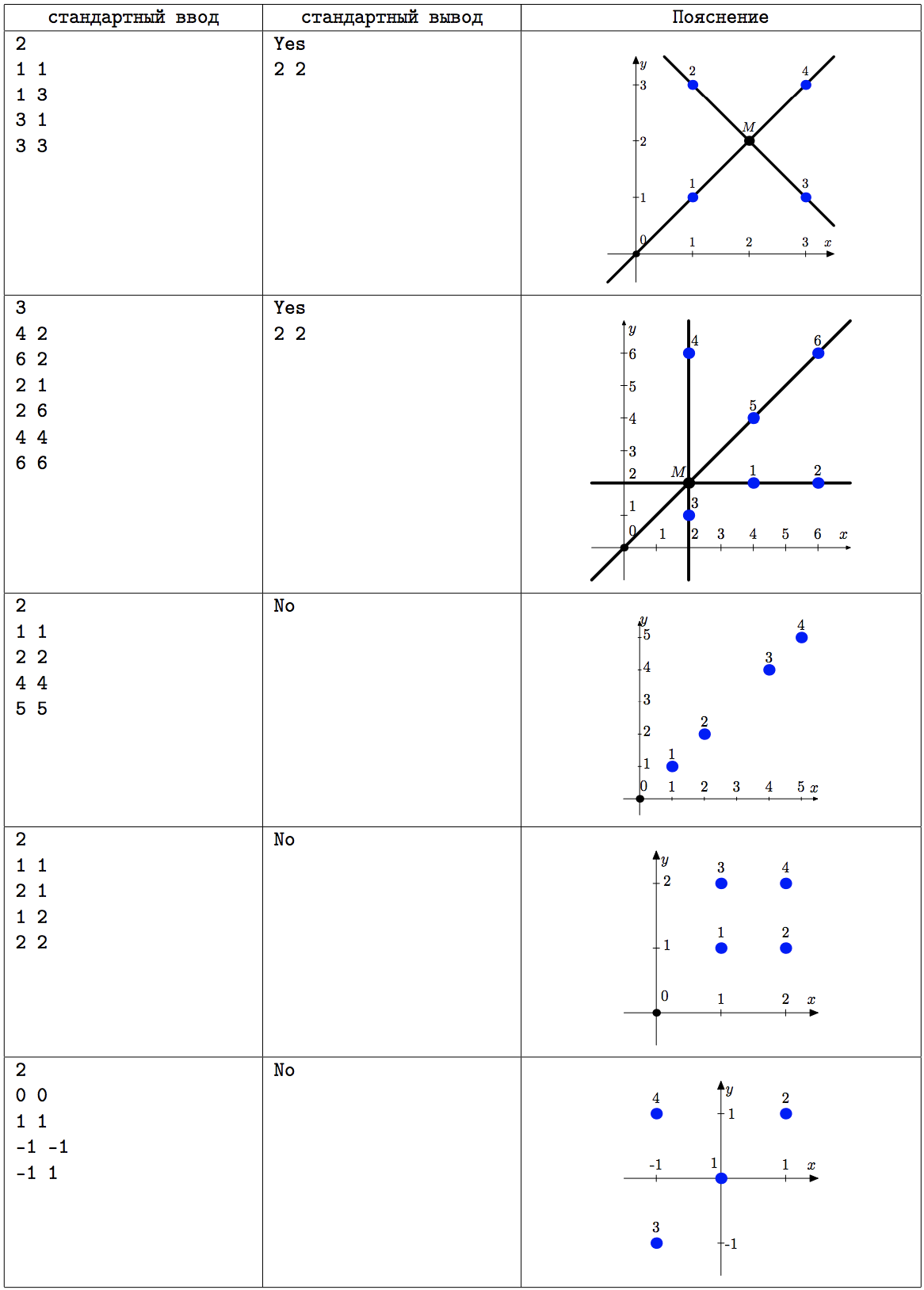
В четвёртом тесте из условия центр Луны мог располагаться только в точке (1.5, 1.5) , но эта точка обладает нецелыми координатами, поэтому ответа нет.
В пятом тесте из условия невозможно найти подходящую точку, которая бы не являлась при этом центром звезды.
Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.