Задача №113917. Робомарафон
В робомарафоне принимают участие n роботов. Роботы должны преодолеть одинаковую дистанцию, передвигаясь по расположенным рядом друг с другом дорожкам шириной один метр каждая. Известно, что расположенный на i -й дорожке робот преодолевает дистанцию за a i секунд.
В точке старта каждого робота установлено специальное сигнальное устройство, которое должно сработать в момент старта. Чтобы сделать соревнования менее предсказуемыми, судьи перед стартом могут отключить некоторые сигнальные устройства, остальные устройства останутся активными . Только активные устройства срабатывают в тот момент, когда главный судья начинает робомарафон. В начале робомарафона хотя бы одно сигнальное устройство должно являться активным.
Каждый робот начинает движение в тот момент, когда до него доходит стартовый сигнал от активного устройства. Сигнал распространяется со скоростью 1 метр в секунду. Расстояние между дорожками i и j равно | i - j | метров. Обозначим как x i расстояние от i -й дорожки до ближайшей дорожки, содержащей активное устройство. Робот на i -й дорожке начнёт движение через x i секунд после старта, преодолеет дистанцию за a i секунд, и финиширует через f i = a i + x i секунд после старта робомарафона.
Пусть k i — количество роботов, которые финишировали строго раньше i -го робота. Место i -го робота по итогам робомарафона равно k i + 1 . Если несколько роботов финишируют одновременно, а перед ними финишировали k роботов, то считается, что все они заняли ( k + 1) -е место.
Рассмотрим пример. Пусть n = 3 , роботы преодолевают дистанцию за a 1 = 2 , a 2 = 3 и a 3 = 5 секунд, а активным являлось только сигнальное устройство у третьего робота. Тогда первый робот начнёт движение через 2 секунды после начала забега, f 1 = 4 . Второй робот начнёт движение через 1 секунду, f 2 = 4 . Третий робот начнёт движение в момент старта, f 3 = 5 . По итогам забега первый и второй робот делят первое место, третий робот занимает третье место. Если же, например, сработают все три сигнальных устройства, роботы финишируют через f 1 = 2 , f 2 = 3 , f 3 = 5 , секунд, соответственно. Первый робот займёт первое место, второй робот займёт второе место, а третий робот — третье место.
Как видно из примера, место, которое займёт робот, зависит от того, какие сигнальные устройства являются активными. Необходимо обрабатывать два типа запросов:
- для каждого робота определить минимальное место, которое он может занять;
- для каждого робота определить максимальное место, которое он может занять.
Требуется написать программу, которая по типу запроса и информации о времени прохождения дистанции каждым роботом определяет для каждого робота минимальное или максимальное место, которое он может занять в робомарафоне.
В первой строке входных данных находятся два целых числа: n — количество роботов ( 1 ≤ n ≤ 400 000 ), и p — тип запроса. Значение p = 1 означает, что для каждого робота необходимо определить минимальное место, которое он может занять, значение p = 2 означает, что для каждого робота необходимо определить максимальное место, которое он может занять.
Во второй строке находятся n целых чисел a 1 , a 2 , ..., a n — время, за которое роботы преодолевают дистанцию ( 0 < a i ≤ 10 9 ).
Требуется вывести n целых чисел, i -е из которых, в зависимости от типа запроса, должно задавать минимальное или максимальное место, которое может занять i -й робот.
Группа тестов для подзадачи 3 включает 30 тестов. Каждый из этих тестов оценивается независимо в 1 балл.
Группа тестов для подзадачи 4 включает 50 тестов. Каждый из этих тестов оценивается независимо в 1 балл.
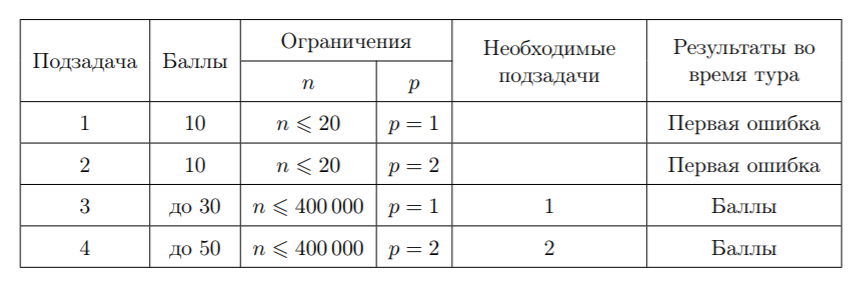
Значения n для всех тестов в подзадаче 3 приведены в следующей таблице.
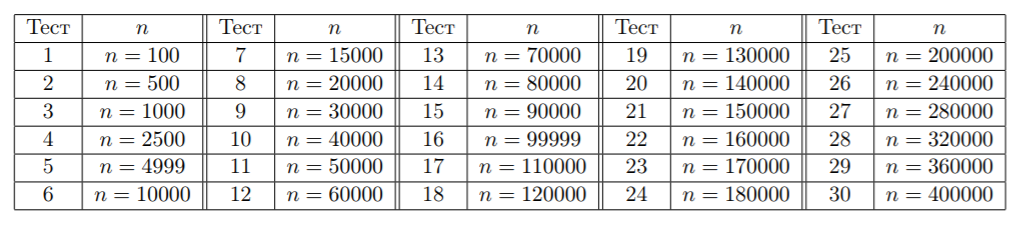
Значения n для всех тестов в подзадаче 4 приведены в следующей таблице.
5 1 8 5 5 7 7
3 1 1 2 1
5 2 8 5 5 7 7
5 3 2 4 5