Задача №114034. Вкусные тортики
Каждый день летних каникул Миша рисовал в блокнотике аккуратное прямоугольное поле размером N × M клеточек и закрашивал на нём некоторые клеточки. Отметим, что каждый день у Миши получалась новая картинка, непохожая на другие, таким образом, всего у Миши получилось 2 NM картинок (на рисунке ниже закрашенные клетки обозначены серым).
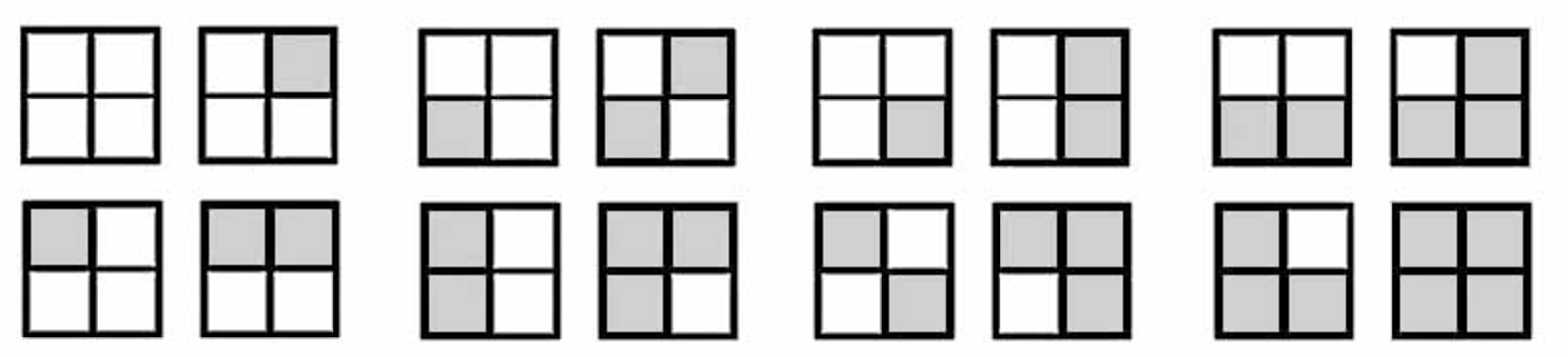
Каждый день его друг Володя помогал Мише скрасить тяжелые будни: он брал очередной Мишин рисунок и пытался покрыть незакрашенные клетки этого рисунка прямоугольниками размера 1 × 2 (при этом каждая незакрашенная клеточка рисунка должна быть покрыта, прямоугольник не может накрывать закрашенную клеточку, прямоугольники не могут вылезать за пределы поля или перекрываться).

Конечно, Володе не всегда удавалось это сделать (те случаи, в которых ему удалось это сделать при N = 2 и M = 2 изображены на рисунке выше). Но в те немногие дни, когда это происходило, мама Миши очень радовалась за ребят и пекла им тортик. Сколько же тортиков пришлось ей испечь?
В первой строке входных данных содержится два целых числа N и M — размеры поля ( {1 ≤ N ≤ 6} , {1 ≤ M ≤ 500} ).
Выведите единственное число — искомое количество тортиков по модулю 10 9 + 7 .
Тесты к этой задаче состоят из трех групп.
- Тесты 1–2. Тесты из условия, эта группа оценивается в ноль баллов.
- Тесты 3–14. В тестах этой группы N · M ≤ 10 . Эта группа оценивается в 20 баллов.
- Тесты 15–20. В тестах этой группы N · M ≤ 20 . Эта группа оценивается в 30 баллов.
- В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 50 баллов. Решение будет тестироваться на тестах этой группы offline, т. е. после окончания тура.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы. Тестирование на тестах каждой группы производится только в случае прохождения всех тестов из всех предыдущих групп.
2 2
6
2 3
18