Задача №114046. Олимпиада
Маленький мальчик Гриша уже сам начал делать олимпиады, и ему как раз нужно подготовить Открытую Олимпиаду по Информатике. Для олимпиады нужно придумывать задачи, а Гриша как раз очень любит этим заниматься. Каждую задачу он характеризует ее сложностью, которая является неотрицательным целым числом. Сложность олимпиады Гриша оценивает как сумму сложностей всех задач в ней.
На Открытую Олимпиаду по Информатике Грише требуется придумать \(n\) задач. Конечно, Гриша еще не дорос до того, чтобы составлять олимпиаду самому, поэтому за его действиями следит многоуважаемое начальство. Начальство любит отвергать некоторые задачи, но Гриша знает, что оно не может отклонить больше, чем \(k\) из его задач. Также Гриша, исходя из своего большого опыта, считает, что давать олимпиаду со сложностью меньше чем \(x\) будет бессмысленно, поэтому он не допустит такого.
Как мы уже говорили, Гриша — настоящий специалист в придумывании задач и может придумать сколько угодно задач любой сложности. Он хочет придумать \(n\) задач, понимая, что часть из них могут отклонить, и, конечно, он хочет, чтобы независимо от того, какие задачи его начальство отвергнет, сложность олимпиады из оставшихся задач была не меньше \(x\). Конечно, Гриша является еще и лентяем, поэтому не хочет перетруждаться и планирует придумать \(n\) задач с минимальной суммарной сложностью. К сожалению, сейчас он занят учебой и не может расчитать минимальную суммарную сложность этих задач. Помогите Грише, ведь до олимпиады осталось не так много времени.
В первой строке заданы три целых числа \(n\), \(k\) и \(x\) (\(2 \le n \le 10^9\), \(1 \le k \lt n\), \(1 \le x \le 10^9\)) — количество задач, которое хочет придумать Гриша, максимальное количество задач, которое может отвергнуть его начальство и минимальная допустимая сложность контеста по мнению Гриши.
Выведите одно целое число — минимальную суммарную сложность придуманных Гришей задач.
В первом тесте из условия Гриша должен придумать три задачи, при этом начальство может отклонить одну из них, а сложность олимпиады должна быть не меньше 5. В таком случае Гриша может придумать две задачи сложности 3 и одну задачу сложности 2. Тогда, какую бы задачу ни отвегнуло начальство, сложность контеста будет равна 5 или 6, а суммарная сложность всех задач, придуманных Гришей, будет равна 8.
Во втором тесте из условия Гриша может придумать все три требуемые задачи со сложностью 1 и, какие бы две жюри ни выкинуло, оставшийся контест будет иметь сложность не менее 1. В таком случае суммарная сложность задач, придуманных Гришей будет равна 3.
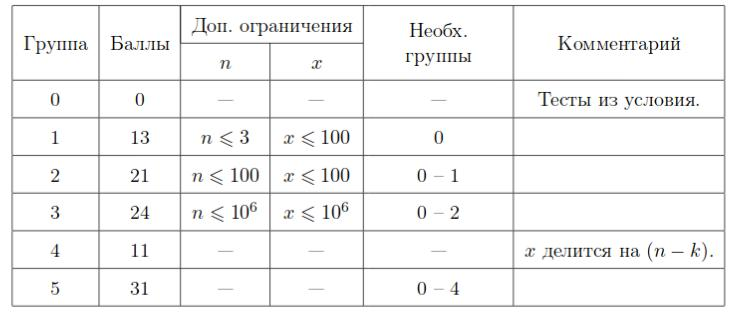
Тесты к этой задаче состоят из пяти подзадач. Баллы за каждую подзадачу ставятся только при прохождении всех тестов подзадачи и всех тестов необходимых подзадач.
3 1 5
8
3 2 1
3