Задача №114048. Метро
Пафнутий решил использовать метро, чтобы достичь своей цели.
Чтобы пройти через турникет, надо использовать специальную карточку SLON (Subterranean Lowcost Orientational Network). У каждой карточки есть неотрицательный целый баланс — количество бурлей, которые записаны на карточке. Если на карточке есть хотя бы \(k\) бурлей, то пройти через турникет возможно, после чего баланс карточки уменьшается на \(k\) бурлей. Если же на карточке меньше \(k\) бурлей, то Пафнутий не сможет ей воспользоваться, чтобы пройти через турникет.
Изначально у Пафнутия есть \(n\) карточек, баланс карточки с номером \(i\) составляет \(a_i\) бурлей. Также Пафнутий накопил \(p\) бурлей и может как угодно распределить эти деньги между карточками. Формально, пусть Пафнутий к балансу карточки с номером \(i\) добавил \(add_i \ge 0\) бурлей, тогда должно выполняться условие \(add_1 + add_2 + \ldots + add_n \le p\). Возможности перераспределять деньги между карточками нет, то есть баланс карточки может увеличиваться только за счет какой-то части из этих \(p\) бурлей и уменьшаться только при проходе через турникет.
Пафнутий не очень любит математику. Помогите ему определить, какое максимальное количество раз он сможет поехать на метро, если распределит \(p\) бурлей по карточкам оптимально.
В первой строке заданы три целых числа \(n\), \(p\) и \(k\) (\(1 \leq n \leq 10^5\), \(0 \leq p \leq 10^{18}\), \(1 \leq k \leq 10^9\)) — количество карточек, накопленная сумма и плата за один проход через турникет, соответственно.
Во второй строке задано \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(0 \leq a_i \leq 10^9\)) — балансы карточек.
Выведите одно целое число — максимальное количество раз, которое Пафнутий сможет поехать на метро.
В первом примере из условия изначально можно поехать только 3 раза. Но если добавить 1 бурль на первую, вторую или третью карточку, то Пафнутий сможет поехать на метро 4 раза.
Во втором примере 1000 бурлей хватит только для того, чтобы сделать баланс обеих карточек равным 2000 бурлям.
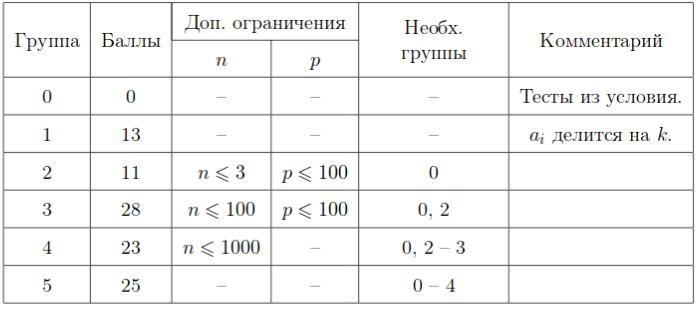
Тесты к этой задаче состоят из пяти подзадач. Баллы за каждую подзадачу ставятся только при прохождении всех тестов подзадачи и всех тестов необходимых подзадач.
5 1 4 7 7 3 4 1
4
2 1000 2000 1299 1701
2