Задача №114049. Дима и массив
Диме не дарили массив \(a\), состоящий из \(n\) целых чисел на день рождения, он не покупал его, не находил на улице, а он у него просто есть и всегда был, и Диме не очень-то и интересно откуда.
Дима не играет с массивом, не дарит его Пете, не режет на кусочки и не стремится его уничтожить. Дима просто выполняет операции двух видов со своим массивом:
- ? l r — узнать MEX мультимножества \(\{a_l, a_{l+1}, \ldots, a_r\}\)
- ! i x — присвоить \(a_i\) значение \(x\) \((0 \leq x \leq n)\)
MEX мультимножества чисел \(\{a_1, a_2, \ldots, a_k\}\) — это минимальное целое \(t \ge 0\) такое, что \(t \ne a_i\) для всех \(1 \leq i \leq k\).
На самом деле, Диме не очень нравится выполнять операции двух видов со своим массивом. Диму волнуют лишь результаты операций первого типа. Помогите Диме и напишите программу, которая выполнит операции за него.
Первая строка содержит два целых числа \(n\) и \(q\) (\(1 \leq n \leq 500\,000, 1 \leq q \leq 250\,000\)) — размер массива, который есть у Димы и количество операций, соответственно.
Вторая строка содержит \(n\) целых чисел \(a_i\) (\(0 \leq a_i \leq n\)) — массив Димы до начала операций.
Каждая из следующих \(q\) строк содержит описание одной операции в формате, описанном выше.
Гарантируется, что суммарно Дима сделал не более \(50\,000\) операций изменения массива .
Элементы массива пронумерованы, начиная с \(1\).
Для каждой операцияя первого типа выведите одно целое число — MEX соответствующего мультимножества. Ответы на запросы выводите в порядке, в котором они заданы во входных данных.
В примере запросы выглядят следующим образом:
- Изначально массив равен \([4, 1, 0, 2, 2, 3]\)
- В первом запросе считается MEX от \(\{4, 1, 0, 2, 2, 3\}\) и он равен \(5\).
- Во втором запросе считается MEX от \(\{2, 2, 3\}\) и он равен \(0\).
- В третьем запросе считается MEX от \(\{1, 0, 2, 2\}\) и он равен \(3\).
- В четвёртом запросе считается MEX от \(\{1, 0, 2, 2, 3\}\) и он равен \(4\).
- Пятый запрос меняет массив. Теперь он равен \([4, 1, 3, 2, 2, 3]\).
- В шестом запросе считается MEX от всего массива и он равен \(0\).
- Седьмой запрос меняет массив. Теперь он равен \([4, 1, 3, 0, 2, 3]\).
- В восьмом запросе снова считается MEX от всего массива и теперь он равен \(5\).
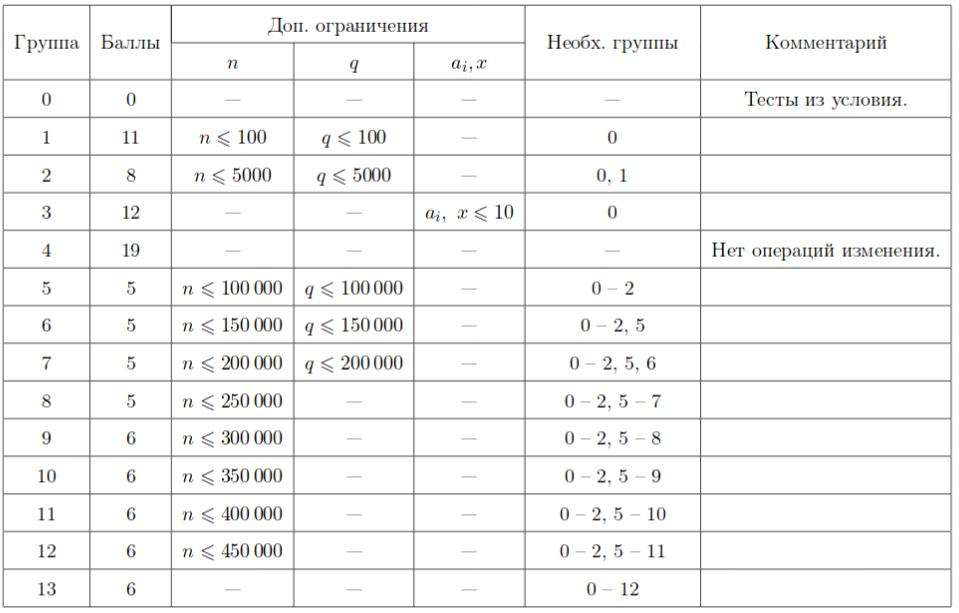
Тесты к этой задаче состоят из тринадцати подзадач. Баллы за каждую подзадачу ставятся только при прохождении всех тестов подзадачи и всех тестов необходимых подзадач.
6 8 4 1 0 2 2 3 ? 1 6 ? 4 6 ? 2 5 ? 2 6 ! 3 3 ? 1 6 ! 4 0 ? 1 6
5 0 3 4 0 5