Задача №114050. Петя и монеты
Филателист Петя отправился в магазин, чтобы приобрести его заветную мечту — настоящую медную монету XVII века. В магазине продавец показал Пете \(n\) монет XVII века, имеющихся в наличии, каждая из которых сделана из одного из трех материалов: железа, меди или бронзы. К сожалению, время не пощадило монеты, поэтому они покрылись ржавчиной, и невозможно определить, какая монета из какого материала сделана. Чтобы Пете было проще найти нужную монету, продавец показал ему \(m\) пар монет таких, что монеты из пары сделаны из различных материалов. Кроме того, продавец сказал Пете, что ровно одна из \(n\) монет сделана из меди. Чтобы заполучить заветную монету, Петя решил приобрести все монеты, которые могут быть медными, исходя из информации, полученной им от продавца.
Более формально, Петя купит монету с номером \(p\) если и только если могло оказаться так, что все монеты с номерами, отличиными от \(p\) сделаны из железа и бронзы, а монета с номером \(p\) сделана из меди и при этом в каждой из \(m\) пар номеров монет, озвученных продавцом, монеты с соответствующими номерами сделаны из разных материалов.
Определите, какие монеты купит Петя.
В первой строке заданы два целых числа \(n\) и \(m\) (\(1 \leq n \leq 3 \cdot 10^6, 0 \leq m \leq 3 \cdot 10^6\)) — количество монет XVII века в магазине и количество пар монет, про которые продавец сказал Пете, что они сделаны из разных материалов.
В следующих \(m\) строках заданы пары целых чисел \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n, a_i \neq b_i\)) — номера монет, которые сделаны из различных материалов. Все пары монет во вводе различны.
Если продавец ошибся и ни одна монета не может быть медной, выведите « 0 » (без кавычек). Иначе в первой строке выведите одно целое число \(x\) — количество монет, которые купит Петя.
Во второй строке выведите \(x\) целых чисел \(c_i\) (\(1 \leq c_i \leq n\)) в порядке возрастания — номера монет, которые купит Петя.
В первом примере:
- Монета с номером \(1\) может быть медной, если, например, монеты с номерами \(2\) и \(3\) железные, а монета с номером \(4\) бронзовая.
- Монета с номером \(2\) может быть медной, если, например, монеты с номерами \(1\) и \(3\) железные, а монета с номером \(4\) бронзовая.
- Монета с номером \(3\) не может быть медной, так как среди монет с номерами \(1\), \(2\) и \(4\) не могут быть только железные и бронзовые.
- Монета с номером \(4\) может быть медной, если, например, монеты с номерами \(2\) и \(3\) железные, а монета с номером \(1\) бронзовая.
Во втором примере любая монета может быть медной, в случае, если, например, другая монета сделана из железа.
В третьем примере продавец ошибся и ни одна монета не может быть медной.
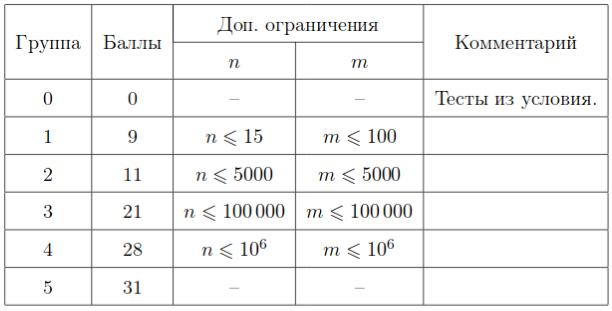
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
4 3 1 2 1 4 4 2
3 1 2 4
2 1 1 2
2 1 2
6 6 1 2 4 5 2 3 5 6 1 3 4 6
0
12 14 1 2 3 2 3 4 5 4 5 6 6 7 3 8 8 9 9 6 2 10 10 12 12 11 11 7 1 7
4 2 3 6 7