Задача №114051. Грустные танцы
Во Флатляндии проводится ежегодный турнир по танцам!
Из города NN приехала команда, состоящая из n танцоров, и вот настал день соревнований.
Состязания проходят в таком формате: танцоры пронумерованы от 1 до n , и изначально i -й танцор стоит на i -м месте. После этого они начинают танцевать по заранее согласованной программе выступления a : каждую минуту танцор с a i -го места передвигается на i -е место, при этом все a i различны. От команды требуется выстроиться так, чтобы i -й танцор оказался на b i -м месте (аналогично, все b i различны). После этого выступление завершается, и жюри оценивает его техничность и артистизм. При этом выступление должно продлиться хотя бы одну минуту, иначе оценивать будет просто нечего.
Но в этом году участники заподозрили жюри в подлоге: к ним пришла мысль, что, возможно, следуя программе a , они никогда не смогут занять требуемое положение b , что приводит к автоматическому поражению в турнире.
Так как они не программисты по образованию, команда города NN решила обратиться к вам за помощью: проверьте по их программе выступления a и требуемому положению b , существует ли такое положительное количество минут k , что через k минут после начала выступления i -й танцор будет находиться на b i -м месте.
В первой строке входного файла содержится целое число n ( 1 ≤ n ≤ 10 6 ) — количество участников команды, приехавшей из города NN .
Вторая строка содержит n целых чисел a 1 , ..., a n ( 1 ≤ a i ≤ n ) — программу выступления a . Гарантируется, что каждое число от 1 до n встречается в a ровно один раз.
Третья строка содержит n целых чисел b 1 , ..., b n ( 1 ≤ b i ≤ n ) — требуемое положение b . Гарантируется, что каждое число от 1 до n встречается в b ровно один раз.
Для каждого тестового примера выведите « Yes » (без кавычек), если существует такое количество минут k , что спустя k минут после начала выступления все танцоры будут в требуемом от них положении, или « No » (без кавычек), если такого k не существует.
В первом примере в нулевой момент времени танцоры располагаются так: 1 2 3 4 . Но так как выступление должно продлиться хотя бы одну минуту, k = 0 не подходит. Далее происходят следующие перемещения:
- 2 3 4 1 после первой минуты
- 3 4 1 2 после второй минуты
- 4 1 2 3 после третьй минуты
- 1 2 3 4 после четвертой минуты
Во втором примере танцоры всегда остаются на своем месте, следственно, они никогда не займут требуемое положение, и ответ — « No ».
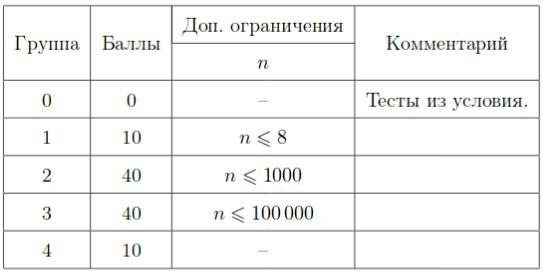
Тесты к этой задаче состоят из четырех групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
4 2 3 4 1 1 2 3 4
Yes
4 1 2 3 4 2 1 4 3
No