Задача №114052. Обмены в перестановке
Дана перестановка \(a\) чисел от \(1\) до \(n\), а также набор из \(m\) пар индексов. За один ход разрешается выбрать одну из этих \(m\) пар и поменять элементы на соответствующих позициях местами (перестановка, соответственно, изменится). Вы можете сделать произвольное количество ходов (в частности, разрешается не делать ни одного хода).
Определим возрастающую подпоследовательность длины \(k\) как набор индексов \(j_1, j_2, \ldots, j_k\), для которых выполняются два условия:
- \(1 \le j_1 \lt j_2 \lt \ldots \lt j_k \le n\);
-
\(a_{j_1} \lt a_{j_2} \lt \ldots \lt a_{j_k}\).
Какой максимально возможной длины наибольшей возрастающей подпоследовательности можно достичь при правильных обменах элементов?
В первой строке заданы два числа \(n\) и \(m\) (\(1 \le n \le 10^4, 0 \le m \le \min(10^5, \frac{n \cdot (n - 1)}{2}\)) — длина перестановки и количество пар позиций, которые можно обменивать между собой.
В следующей строке через пробел заданы \(n\) различных целых чисел \(a_i\) (\(1 \le a_i \le n\)) — элементы перестановки.
Каждая из следующих \(m\) строк содержит по два числа \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n, u_i \neq v_i\)) — индексы позиций, элементы на которых можно менять. Гарантируется, что ни одна пара не встречается дважды.
Выведите одно целое число — максимально возможную длину наибольшей возрастающей подпоследовательности перестановки после обменов.
Рассмотрим перестановку из первого примера.
\([5, 2, 4, 6, 3, 1]\)
Поменяем местами элементы на позициях \(5\) и \(6\).
\([5, 2, 4, 6, \textbf{1}, \textbf{3}]\).
Теперь поменяем местами элементы на позициях \(1\) и \(5\).
\([\textbf{1}, 2, 4, 6, \textbf{5}, 3]\).
Длина наибольшей возрастающей подпоследовательности в такой перестановке равняется \(4\).
Соответствующая подпоследовательность: \([\textbf{1}, \textbf{2}, \textbf{4}, 6, \textbf{5}, 3]\).
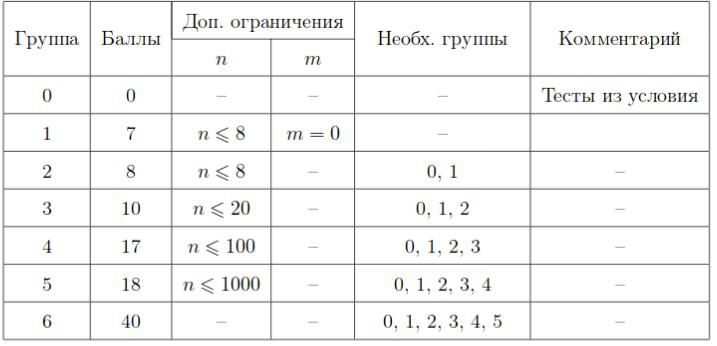
Тесты к этой задаче состоят из шести подзадач. Баллы за каждую подзадачу ставятся только при прохождении всех тестов подзадачи и всех тестов необходимых подзадач.
6 2 5 2 4 6 3 1 5 6 1 5
4
4 2 2 1 4 3 1 3 2 4
3