Задача №114055. Поиск подподстроки в подстроке
Опытным участникам соревнований по спортивному программированию хорошо известна классическая задача о нахождении количества вхождений подстроки в строку. Обычно она формулируется так: дана строка-образец \(s\) и строка \(t\), требуется найти количество индексов, начиная с которых строка \(s\) содержится в строке \(t\).
К сожалению, для решения этой задачи уже придумано множество алгоритмов, поэтому сама по себе она может быть интересна только в качестве упражнения, но не олимпиадной задачи. Однако, как это часто бывает со стандартными задачами, её легко усложнить — представим, что нас интересуют не сами строки \(s\) и \(t\), а некоторые их подстроки \(s[l_1 \ldots r_1]\) и \(t[l_2 \ldots r_2]\).
Как вы уже, наверное, догадались, вам дано \(q\) запросов, \(i\)-й из которых задаёт некоторые подстроки \(\bar s = s[{l_1}_i \ldots {r_1}_i]\) и \(\bar t = t[{l_2}_i \ldots {r_2}_i]\). Для каждого такого запроса необходимо посчитать количество вхождений строки \(\bar s\) в строку \(\bar t\).
Первая и вторая строки входных данных содержат строки \(s\) и \(t\) (\(1 \le |s|, |t| \le 2 \cdot 10^5\)) соответственно. Строки состоят из маленьких букв английского алфавита.
В третьей строке задано одно число \(q\) (\(1 \le q \le 5 \cdot 10^5\)) — количество запросов.
Каждая из следующих \(q\) строк содержит по четыре числа \(l_1\), \(r_1\), \(l_2\) и \(r_2\) (\(1 \le l_1 \le r_1 \le |s|, 1 \le l_2 \le r_2 \le |t|\)), описывающих очередной запрос.
Выведите \(q\) чисел — ответы на запросы.
Рассмотрим запросы в первом примере. Для индексации позиций вхождения будем использовать изначальные позиции в строке \(t\).
- \(\bar s = ab, \bar t = abababa\). \(\bar s\) входит в \(\bar t\), начиная с индексов \([1, 3, 5]\).
- \(\bar s = bb, \bar t = babababb\). \(\bar s\) входит в \(\bar t\), начиная с индекса \([8]\).
- \(\bar s = b, \bar t = baba\). \(\bar s\) входит в \(\bar t\), начиная с индексов \([4, 6]\).
- \(\bar s = ab, \bar t = bab\). \(\bar s\) входит в \(\bar t\), начиная с индекса \([3]\).
- \(\bar s = a, \bar t = ababababb\). \(\bar s\) входит в \(\bar t\), начиная с индексов \([1, 3, 5, 7]\).
Тесты к этой задаче состоят из четырех подзадач. Баллы за каждую подзадачу ставятся только при прохождении всех тестов подзадачи и всех тестов необходимых подзадач.
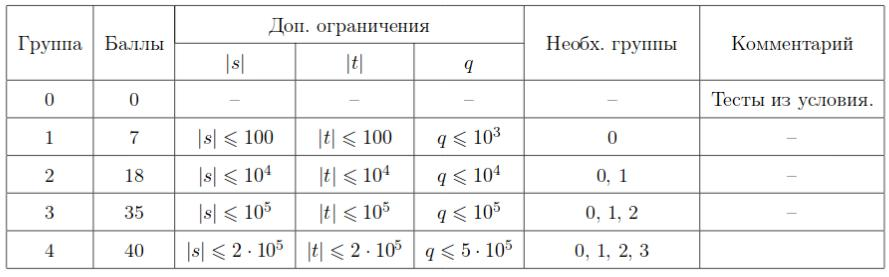
abb ababababb 5 1 2 1 7 2 3 2 9 3 3 4 7 1 2 2 4 1 1 1 9
3 1 2 1 4