Задача №114061. Мухобойка (Meksikanac)
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Пояснение к третьему примеру:
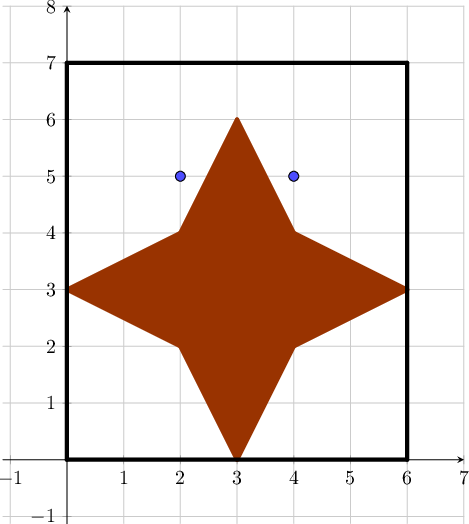
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
4
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
3
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
1