Задача №114096. Декартово
Декартово царство расположено на плоскости, на которой введены декартовы координаты \((x, y)\). Можно считать, что Декартово бесконечно во все стороны.
Царь этого царства хочет построить себе новый дворец. Дворец будет представлять из себя квадрат со сторонами, параллельными осям координат. Дворец может быть сколь угодно большим, царь больше беспокоится о его безопасности.
Всего в Декартово есть \(n\) охранных постов, причём \(i\)-й из них находится в точке \((x_i, y_i)\). Царь может поручить нескольким группам охранников патрулировать границы дворца. Охранники царя способны следовать только достаточно простым указаниям. Каждой группе нужно назначить ровно два различных поста, после чего эта группа будет патрулировать минимальный прямоугольник со сторонами параллельными осям координат, содержащий эти два поста. Этот прямоугольник может иметь нулевую площадь, в частности, если у двух постов группы совпала \(x\) или \(y\) координата. Чтобы избежать путаницы и конфликтов, каждый пост может быть назначен не более чем одной группе.
Чтобы ощущаться достаточное количество безопасности вокруг себя, Царь хочет организовать ровно \(k\) охранных групп, при этом дворец должен быть внутри каждого из патрулируемых прямоугольников, то есть каждая точка дворца должна содержаться внутри или находиться на границе каждого из прямоугольников, патрулируемых какой-либо группой. Помогите Царю выяснить наибольшую возможную сторону дворца, который можно построить и затем чувствовать себя в нём в безопасности.
Первая строка содержит два целых числа \(n\) и \(k\) (\(2 \le n \le 50\,000\), \(1 \le k \le n / 2\)) — количество постов и требуемое количество групп.
Каждая из следующих \(n\) строк содержит два целых числа \(x_i\) и \(y_i\) (\(-10^6 \le x_i, y_i \le 10^6\)) — координаты соответствующего поста.
Гарантируется, что никакие два поста не находятся в одной точке.
Выведите одно число — наибольшую возможную сторону квадратного дворца. Если не существует ни одного дворца ненулевой площади, удовлетворяющего требованиям безопасности, выведите \(0\).
Картинки показывают расположение дворца и охранных маршрутов в первых двух примерах. В третьем примере единственный возможный маршрут образует отрезок, а значит получить ненулевую сторону дворца нельзя.

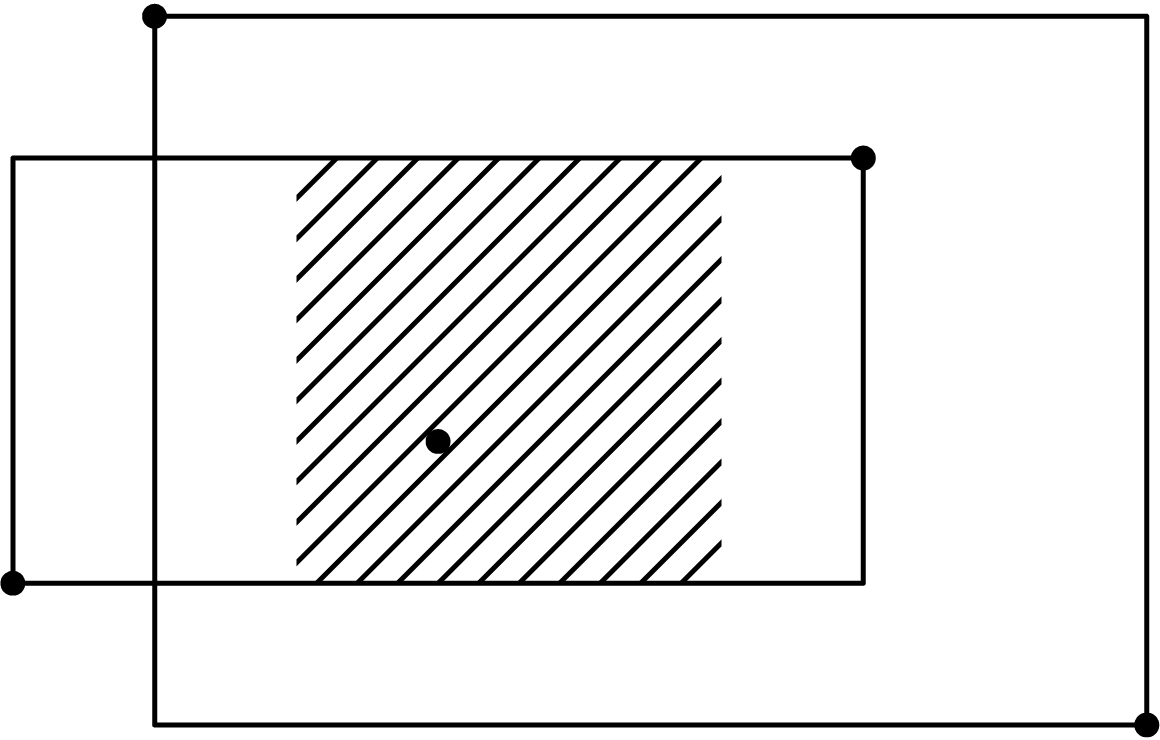
Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

4 1 0 1 3 0 4 3 1 4
2
5 2 4 0 2 4 -4 1 -1 2 -3 5
3
2 1 0 0 10 0
0