Задача №114097. Морской бой
Чтобы разнообразить игру «морской бой» Боря решил добавить в неё новый тип кораблей. Эти корабли состоят из двух прямоугольников. Первый прямоугольник имеет ширину \(w_1\) и высоту \(h_1\), а второй прямоугольник — \(w_2\) и \(h_2\) соответственно. Прямоугольники располагаются один над другим и выровнены по левому краю (см. рисунки после примеров): введём на поле систему координат так, чтобы левая нижняя клеточка первого прямоугольника имела координаты \((1, 1)\). Тогда верхняя правая клеточка первого прямоугольника имеет координаты \((w_1 , h_1)\), левая нижняя клеточка второго прямоугольника имеет координаты \((1, h_1 + 1)\), а правая верхняя клеточка второго прямоугольника имеет координаты \((w_2, h_1 + h_2)\).
По правилам морского боя, после уничтожения корабля необходимо отметить все клеточки, соседние по стороне или углу с клеточками, в которых есть корабль, потому что в этих клеточках уже не могут стоять другие корабли. При этом отмечаются только не принадлежащие кораблю клетки.
Определите, сколько клеток надо будет отметить после уничтожения корабля, придуманного Борей. Поле, на котором, происходит игра, бесконечно во все стороны.
В четырёх строках заданы четыре целых числа \(w_1, h_1, w_2\) и \(h_2\) (\(1 \leq w_1, h_1, w_2, h_2 \leq 10^8\)) — ширина первого прямоугольника, высота первого прямоугольника, ширина второго прямоугольника и высота второго прямоугольника, соответственно.
Выведите одно целое число — количество клеток, которые необходимо закрасить после уничтожения корабля.
В первом примере поле выглядит так (красным обозначен первый прямоугольник, синим обозначен второй прямоугольник, зеленым обозначены отмеченные точки):
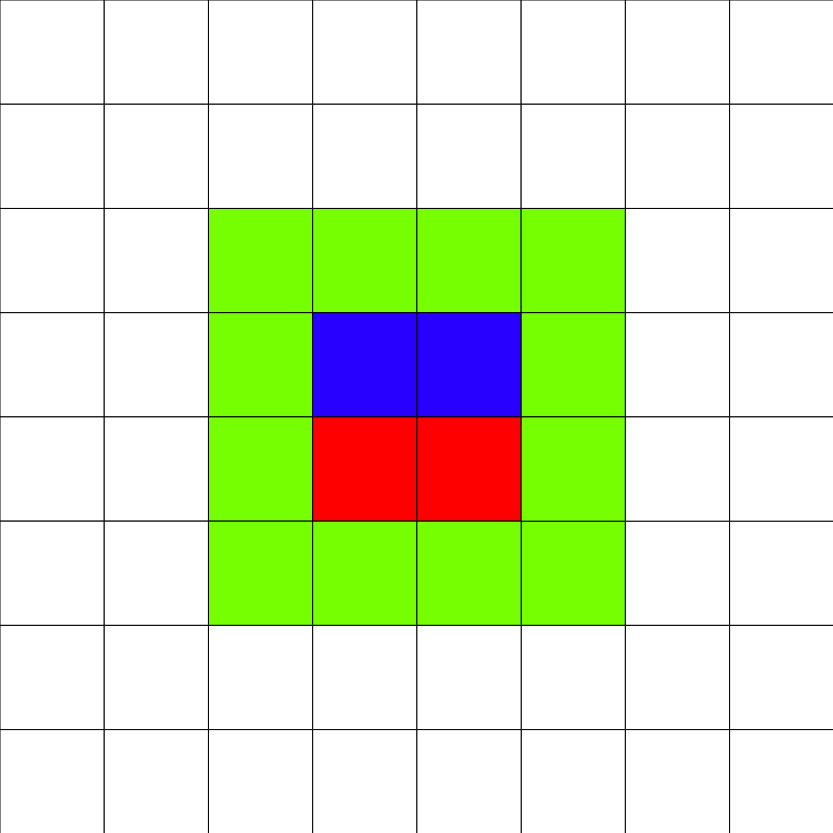
Во втором примере поле выглядит так:
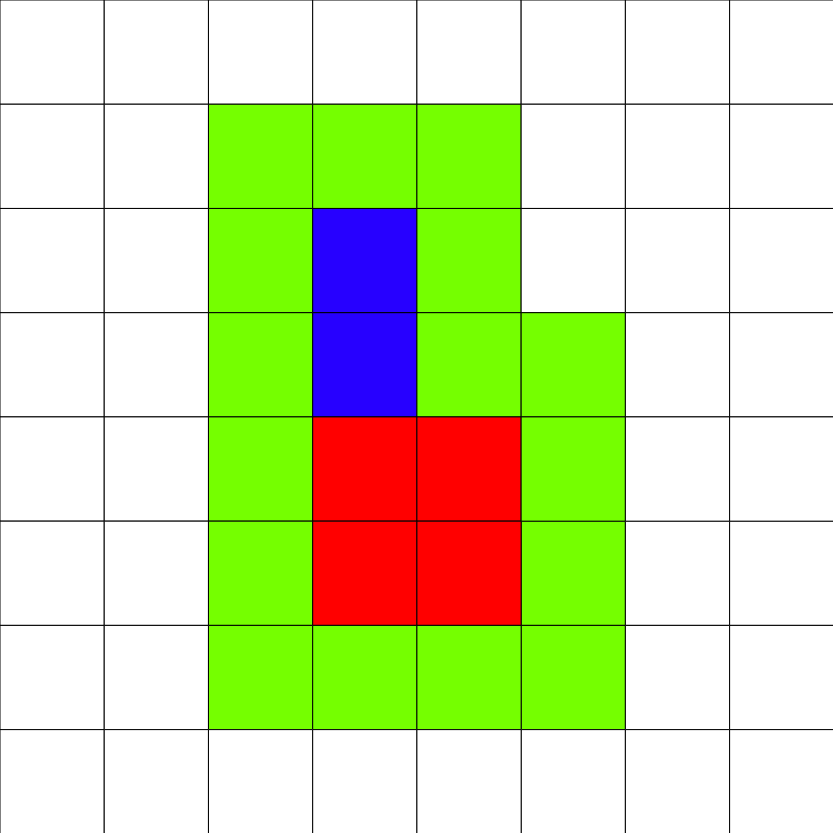
В данной задаче \(20\) тестов, помимо тестов из условия, каждый из них оценивается в \(5\) баллов. Результаты работы ваших решений на всех тестах будут доступны сразу во время соревнования.
Решения, корректно работающие при \(1 \leq w_1, h_1, w_2, h_2 \leq 30\), наберут не менее \(30\) баллов.
Решения, корректно работающие при \(1 \leq w_1, h_1, w_2, h_2 \leq 10^6\), наберут не менее \(75\) баллов.
2 1 2 1
12
2 2 1 2
16