Задача №114102. Ася и котята
Ася очень любит животных. Недавно она приобрела \(n\) котят, дала им числовые идентификаторы от \(1\) до \(n\) и поселила в вольере. Вольер представляет собой ряд из \(n\) ячеек, также пронумерованных от \(1\) до \(n\). Cоседние ячейки разделены сетчатыми перегородками, всего в вольере \(n - 1\) перегородок. Изначально в каждой ячейке поселился ровно один котёнок с некоторым номером.
Наблюдая за котятами, Ася заметила, что они очень дружелюбны и некоторые пары живущих в соседних ячейках котят очень хотят играть друг с другом. Чтобы не лишать их этого удовольствия, Ася стала вынимать перегородки между соседними ячейками, делая их более крупными.
В \(i\)-й день Ася делала следующее.
- Обращала внимание, что какие-то котята \(x_i\) и \(y_i\), в \(i\)-й день живущие в соседних ячейках, хотят играть.
- Удаляла перегородку между этими ячейками, превращая их в одну, в которой оказывались все котята из двух прежних ячеек.
Поскольку Ася не возвращала перегородки, через \(n - 1\) день вольер стал единой ячейкой, в которой обитали все котята. Будучи очень педантичной, Ася записывала в специальный журнал идентификаторы котят \(x_i\) и \(y_i\) для каждого из \(n - 1\) дней.
Вам в руки попал журнал с этой информацией, однако вам неизвестно, как котята были поселены в ячейки изначально. Найдите любое расселение котят по \(n\) исходным ячейкам, не противоречащее данным в журнале.
В первой строке задано целое число \(n\) (\(2 \leq n \leq 150\,000\)) — количество котят.
В следующих \(n - 1\) строках заданы пары целых чисел \(x_i\), \(y_i\) (\(1 \leq x_i, y_i \leq n, x_i \neq y_i\)) — идентификаторы котят, между ячейками которых была удалена перегородка в день \(i\). Гарантируется, что котята \(x_i\) и \(y_i\) не находятся в одной ячейке по итогам предыдущих объединений ячеек.
Выведите \(n\) различных целых чисел \(p_i\) (\(1 \leq p_i \leq n\)), где \(p_i\) — идентификатор котёнка, который изначально жил в ячейке с номером \(i\). Если возможных вариантов ответа несколько, выведите любой из них.
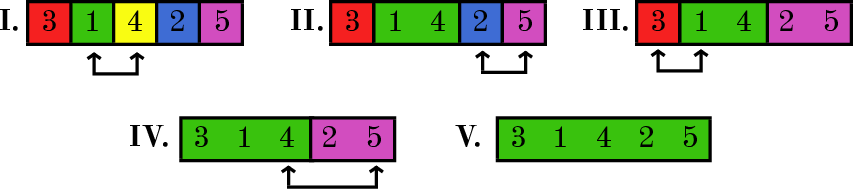
В ответе к примеру приведено одно из возможных изначальных расселений котят, существуют и другие варианты ответа. На изображении ниже показано, как происходило объединение ячеек для этого варианта исходного размещения котят. Обратите внимание, что при таком размещении котята, подружившиеся в каждый из дней согласно журналу Аси, находятся в соседних ячейках.
В данной задаче \(50\) тестов, помимо тестов из условия, каждый из них оценивается в \(2\) балла. Результаты работы ваших решений на всех тестах будут доступны сразу во время соревнования.
Решения, корректно работающие при \(1 \leq n \leq 10\), наберут не менее \(20\) баллов.
Решения, корректно работающие при \(1 \leq n \leq 100\), наберут не менее \(40\) баллов.
Решения, корректно работающие при \(1 \leq n \leq 2000\), наберут не менее \(70\) баллов.
5 1 4 2 5 3 1 4 5
3 1 4 2 5