Задача №114103. Самая опасная акула
Как известно, не только люди любят принимать участие в различных соревнованиях. Среди рыб и моллюсков также проводится множество состязаний на дне океана. Акула Семён участвует в самом престижном соревновании Мирового океана на звание самой опасной акулы. Во время этого состязания акулы соревнуются в различных дисциплинах: плавание на скорость, маскировка, навигация по картам и многим другим. Сейчас Семён проходит испытание под названием «разрушение».
Во время этого испытания перед акулой ставят \(m\) доминошек. Все доминошки стоят на одной прямой, однако высоты доминошек могут различаться. Расстояние между соседними доминошками равно \(1\). Кроме того, у каждой доминошки есть своя стоимость, выраженная целым числом. Цель акулы — уронить все доминошки. Для этого акула может толкнуть любую доминошку влево или вправо, после чего она начнёт падать в этом направлении. Если во время падения доминошка задевает другие, они также начинают падать в ту же сторону, в которую падала исходная, таким образом начинается цепная реакция, в результате которой может упасть множество доминошек. Падающая доминошка задевает другую, если и только если расстояние между ними строго меньше высоты падающей доминошки, причем доминошки не обязательно должны быть соседними.
Разумеется, любая акула справится с тем, чтобы уронить все доминошки таким образом, поэтому оценивается не факт разрушения, а его стоимость. Стоимостью разрушения называется сумма стоимостей доминошек, которые акуле придётся толкнуть, чтобы все доминошки упали.
Семён уже победил в прошлых испытаниях, однако недостаточно умён, чтобы победить в этом. Помогите Семёну и определите, какая минимальная суммарная стоимость доминошек, которые ему придётся толкнуть, чтобы все доминошки упали.
Для уменьшения размера ввода высоты и стоимости доминошек задаются при помощи блоков.
В первой строке заданы два целых числа \(n\) и \(m\) (\(1 \leq n \leq 250\,000, 1 \leq m \leq 10^7\)) — количество блоков и суммарное количество доминошек, которые надо уронить Семёну, соответственно.
Затем следует описание \(n\) блоков. Описание каждого блока состоит из трёх строк.
В первой строке описания блока с номером \(i\) содержится целое число \(k_i\) (\(1 \leq k_i \leq 250\,000, \sum_{i = 1}^{n}{k_i} \leq 250\,000\)) — количество доминошек в блоке.
Во второй строке описания блока с номером \(i\) содержатся \(k_i\) целых чисел \(a_{i, j}\) (\(1 \leq a_{i, j} \leq m\)) — высоты доминошек в блоке.
В третьей строке описания блока с номером \(i\) содержатся \(k_i\) целых чисел \(c_{i, j}\) (\(1 \leq c_{i, j} \leq 100\,000\)) — стоимости доминошек в блоке.
Далее следует описание последовательности доминошек, которые надо уронить Семёну, в порядке слева направо.
В первой строке описания последовательности задано целое число \(q\) (\(n \leq q \leq 250\,000\)) — количество блоков в последовательности доминошек, которые надо уронить.
В следующих \(q\) строках содержатся пары целых чисел \(id_i\) \(mul_i\) (\(1 \leq id_i \leq n, 1 \leq mul_i \leq 100\,000\)), обозначающие, что очередные \(k_{id_i}\) в порядке слева направо доминошек — это доминошки блока \(id_i\), чьи стоимости были умножены на число \(mul_i\).
Гарантируется, что \(\sum_{i = 1}^{q}{k_{id_i}} = m\), а также, что каждый блок встречается хотя бы один раз в последовательности доминошек, которые требуется уронить, то есть для всех \(i\) от \(1\) до \(n\) найдется \(j\) такое, что \(id_j = i\).
Выведите одно целое число — минимальную суммарную стоимость доминошек, которые надо толкнуть, чтобы все доминошки упали.
В первом примере перед Семёном стоят \(7\) доминошек. Их высоты равны \([3, 1, 2, 2, 1, 2, 2]\), а стоимости равны \([4, 3, 6, 3, 1, 2, 1]\). Сначала Семёну следует уронить доминошку с номером \(7\) влево, она упадёт и заденет доминошку с номером \(6\). Доминошка \(6\), падая, заденет доминошку с номером \(5\), которая упадёт, но не заденет другие доминошки. Затем Семён должен уронить доминошку с номером \(1\) вправо, она, падая, заденет доминошки с номерами \(2\) и \(3\), а доминошка \(3\), падая, заденет доминошку \(4\), таким образом все доминошки упадут.
Во втором примере перед Семёном стоит одна доминошка стоимостью \(10000000000\).
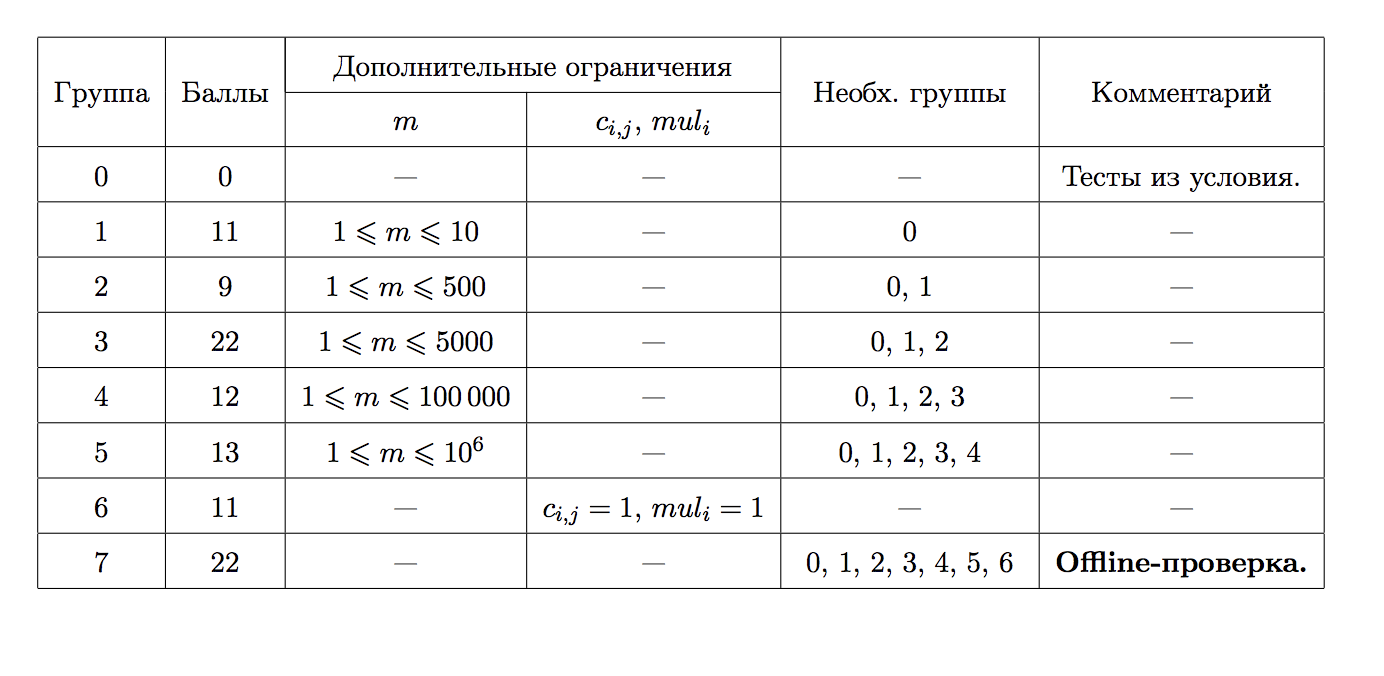
Тесты к этой задаче состоят из семи групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
2 7 3 1 2 2 1 2 1 1 3 2 3 2 2 1 3 1 1
5
1 1 1 1 100000 1 1 100000
10000000000