Задача №114115. Недалёкие строки
Сегодня на уроке строковедения профессор Моррис рассказывал студентам различные способы вычисления расстояния между двумя строками. Один из способов был следующий, пусть имеются две строки
s
и
t
длины
n
, состоящие только из десятичных цифр. Тогда
цифровым
расстоянием между двумя данными строками профессор Моррис считает сумму модулей разности цифр на одинаковых позициях, то есть
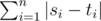, где
s
i
означает цифру, записанную на позиции
i
в строке
s
, а
t
i
означает цифру, записанную на позиции
i
в строке
t
.
В качестве домашнего задания профессор дал каждому студенту строку длины n и поручил выписать все строки длины n (а это целых 10 n строк) в порядке неубывания цифрового расстояния до данной строки. При равенстве расстояния до двух строк, их следует сравнивать лексикографически.
Поскольку у профессора мало времени, чтобы проконтролировать выполнение всего задания каждым из студентов, он дополнительно сообщил каждому из них число k и просит лишь сказать ему строку, находящуюся на k -м месте в выписанной последовательности. Студенты не горят желанием выполнять вручную столь объёмное и монотонное задание, поэтому попросили вас написать программу, которая будет выводить ответ по заданной строке и числу k .
В первой строке входных данных записаны два целых числа n и k ( 1 ≤ n ≤ 200 000 , 1 ≤ k ≤ min (10 n , 10 18 ) ) — длина строки, выданной профессором, и интересующая профессора позиция в итоговой последовательности.
Во второй строке записана строка, состоящая из n десятичных цифр.
Выведите строку из n десятичных цифр, которая будет записана на k -м месте в интересующей профессора последовательности.
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
Во втором примере первые семь слов списка это « 00000 », « 00001 », « 00010 », « 00100 », « 01000 », « 10000 » и « 00002 ».
Слово x 1 , x 2 , ..., x a не превосходит слова y 1 , y 2 , ..., y b в лексикографическом порядке если верно одно из двух условий:
- либо a ≤ b и x 1 = y 1 , ..., x a = y a , то есть первое слово является префиксом второго;
- либо есть такая позиция 1 ≤ j ≤ min ( a , b ) , что x 1 = y 1 , ..., x j - 1 = y j - 1 и x j < y j , то есть, в первой позиции, в которой слова отличаются, в первом слове стоит меньшая буква.
5 1 00000
00000
5 7 00000
00002
3 44 132
212