Задача №114116. Блуждания в большом городе
Город N состоит из n перекрёстков и m соединяющих их двусторонних дорог. Известно, что из любого перекрёстка выходят хотя бы две дороги, и что, используя данную сеть дорог, можно дойти от любого перекрёстка до любого другого перекрёстка. Дополнительно известно, что любые два перекрёстка напрямую соединены не более, чем одной дорогой.
Студент только что вышел из увеселительного заведения, расположенного рядом с перекрёстком s , и направляется в свой дом, расположенный рядом с перекрёстком t . Каждую минуту происходит следующее:
- Студент выбирает одну из дорог, начинающихся от перекрёстка, где он сейчас находится, и идёт вдоль этой дороги.
- Если он оказался в перекрёстке с номером t , то он немедленно идёт домой и ложится спать.
- В противном случае под неожиданным воздействием непреодолимой жажды приключений он выбирает какую-то случайную дорогу, начинающуюся от текущего перекрёстка, и идёт вдоль неё. Единственное ограничение состоит в том, что он никогда не выберет дорогу, вдоль которой он только что попал на данный перекрёсток (то есть использовал её в пункте 1 текущей минуты).
- Если после этого действия он оказался на перекрёстке t , то он идёт домой.
По заданному описанию дорожной сети города и номерам перекрёстков s и t определите, верно ли что студент сможет гарантированно попасть домой за конечное число шагов. Если это так, то определите минимальное число x , такое что студент сможет оказаться дома за не более, чем x минут, вне зависимости от того, какие случайные решения он будет принимать в пункте 3 каждой минуты.
В первой строке входных данных записано целое число t ( 1 ≤ t ≤ 100 000 ) — количество тестовых примеров во входных данных. Далее следует t описаний тестовых примеров.
В первой строке каждого описания тестового примера записаны четыре целых числа n , m , s и t ( 3 ≤ n , m , ≤ 300 000 , 1 ≤ s , t ≤ n , s ≠ t ) — количество перекрёстков и количество дорог в городе N, а также перекрёсток, рядом с которым студент начинает, и перекрёсток, куда он хочет попасть, соответственно.
В i -й из последующих m строк записаны два целых числа u i и v i ( 1 ≤ u i , v i ≤ n , u i ≠ v i ) — номера двух перекрёстков, соединённых i -й двусторонней дорогой. Гарантируется, что из любого перекрёстка можно добраться до любого другого перекрёстка, перемещаясь только вдоль указанных дорог, из любого перекрёстка выходит не менее двух дорог, и никакие две дороги не соединяют одну и ту же пару перекрёстков.
Гарантируется, что суммарное количество перекрёстков и суммарное количество дорог по всем тестовым примерам оба не превысят 1 000 000 .
Для каждого из t тестовых примеров выведите одно целое число. Если студент может бесконечно долго блуждать по городу, совершая неудачные случайные выборы, то выведите - 1 . В противном случае выведите минимальное количество минут, за которое студент сможет гарантированно добрать до дома, если будет делать оптимальный выбор на шаге 1 каждой минуты.
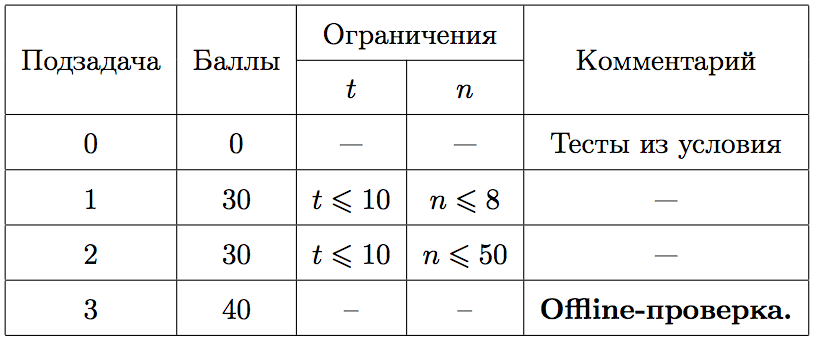
Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
В первом примере студент первым ходом идёт к перекрёстку номер 3 , затем случайно выбирает дорогу к перекрёстку 2 или перекрёстку 4 . В случае выбора дороги к перекрёстку 2 он немедленно оказывается дома. В противном случае, он идёт к перекрёстку рядом с домом в начале следующей минуты.
Во втором примере студент всё время может блуждать между парой перекрёстков (2, 3) и парой перекрёстков (4, 5) . Каждый раз, когда он пойдёт в сторону перекрёстка 4 или 5 , он может сделать неудачный случайный выбор и оказаться на перекрёстке 2 или перекрёстке 3 .
2 4 5 1 2 1 3 1 4 3 4 2 4 2 3 6 9 1 6 1 2 1 3 2 3 2 4 2 5 3 4 3 5 4 6 5 6
2 -1