Задача №114120. Кооперативная игра
Миша очень любит играть в кооперативные игры с неполной информацией. Сегодня он предложил десяти своим друзьям сыграть в кооперативную игру «Озеро».
Миша уже нарисовал игровое поле для предстоящей игры. Оно представляет из себя ориентированный граф, состоящий из двух частей. Одна из этих частей — дорожка вдоль берега озера, являющаяся циклом из \(c\) вершин. Вторая часть — тропинка от домика к озеру, представляющая из себя цепь из \(t\) вершин, причём из последней вершины этой цепи проведено ребро в одну из вершин дорожки вокруг озера — в ту, из которой на озеро открывается наилучший вид. Игровое поле Миша решил держать в секрете, так что никто кроме него не знает ни \(t\), ни \(c\).
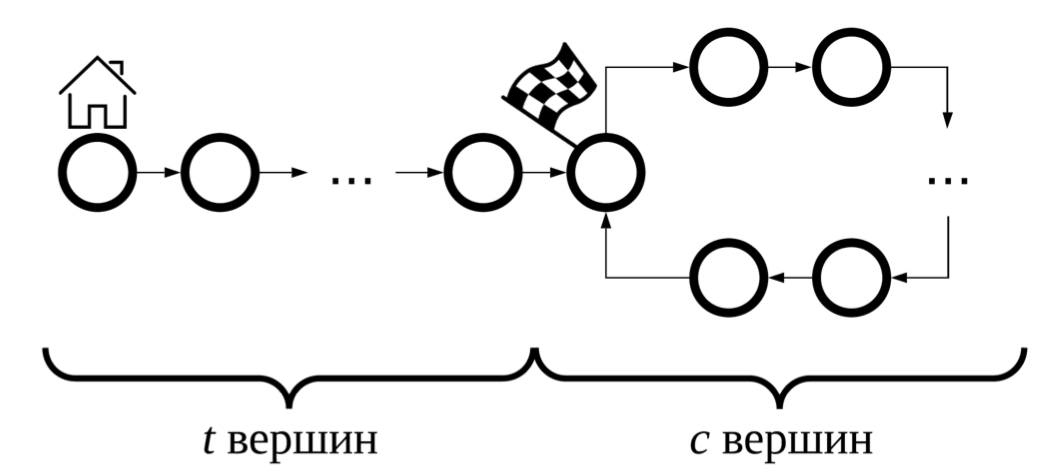
В начале игры игровые фишки всех десяти игроков, для удобства пронумерованных цифрами от \(0\) до \(9\), располагаются в начале тропинки, в вершине у домика. Затем не более \(q\) раз Миша будет одновременно передвигать в следующие вершины фишки игроков, высказавших такое желание на этом ходу, а после этого объявлять, фишки каких игроков находятся в одной вершине, а каких — в разных. Обратите внимание, что у каждой вершины игрового поля есть только одна следующая, при этом каждая кроме стартовой и вершины с лучшими видами является следующей только для одной вершины. Стартовая вершина не является следующей ни для какой вершины, а вершина с лучшими видами является следующей для последней вершины цепочки и для одной из вершин цикла. Мише так понравилась идея не сообщать друзьям \(t\) и \(c\), что и \(q\) он решил тоже не объявлять.
Цель игры — перевести игровые фишки всех игроков в вершину с наилучшим видом на озеро, то есть в ту, которая отмечена финишным флагом. Мишины друзья не представляют, как можно выиграть в такой игре не зная ни \(c\), ни \(t\), ни \(q\), но, к счастью для них, они ещё и ваши друзья. Помогите им: скоординируйте их действия так, чтобы победить.
Для удобства пронумеруем друзей Миши целыми числами от \(0\) до \(9\) включительно.
Для того, чтобы отдать команды перемещения друзьям, выведите « next » а затем через пробел номера друзей, которым необходимо отдать команды. Например, чтобы отдать команду перемещения друзьям с номерами \(0\), \(2\), \(5\) и \(9\) выведите « next 0 2 5 9 ». На каждом ходу обязательно перемещать хотя бы одного из друзей.
В качестве ответа проверяющая программа выдаст сначала число \(k\), а потом \(10\) цифр, разбитых на \(k\) групп, разделённых пробелами. Друзья, соответствующие цифрам, находящимся в одной группе, находятся в одной вершине. Друзья, соответствующие цифрам, находящимся в разных группах, находятся в разных вершинах. Цифры в каждой группе следуют в порядке возрастания.
Например ответ проверяющей программы « 2 05 12346789 » означает, что друзья с номерами \(0\) и \(5\) находятся в одной вершине, а все остальные друзья в одной и той же, но другой вершине. Ответ проверяющей программы « 4 01 567 234 89 » означает, что друзья Миши находятся в четырёх различных вершинах: в первой находятся друзья с номерами \(0\) и \(1\), во второй — друзья с номерами \(5\), \(6\) и \(7\), в третьей — друзья с номерами \(2\), \(3\) и \(4\), а в четвёртой — друзья с номерами \(8\) и \(9\).
Если вы превысите лимит на количество ходов или нарушите протокол взаимодействия, то вместо информации о местоположении друзей вашей программе на вход будет передана строка « stop ». Считав такую строку, ваша программа должна немедленно завершить работу, иначе она может получить вердикт тестирования, отличный от настоящего.
После того, как все друзья соберутся в вершине с лучшим видом необходимо вывести « done » и завершить работу программы.
После вывода каждой строки сбрасывайте буфер вывода — для этого используйте flush(output) на языке Паскаль или Delphi, fflush(stdout) или cout.flush() в C/C++, sys.stdout.flush() на языке Python, System.out.flush() на языке Java.
В условии в примере взаимодействия вводимые и выводимые данные расположены для удобства восприятия в хронологическом порядке, при реальном взаимодействии никакие «лишние» переводы строк возникать не должны.
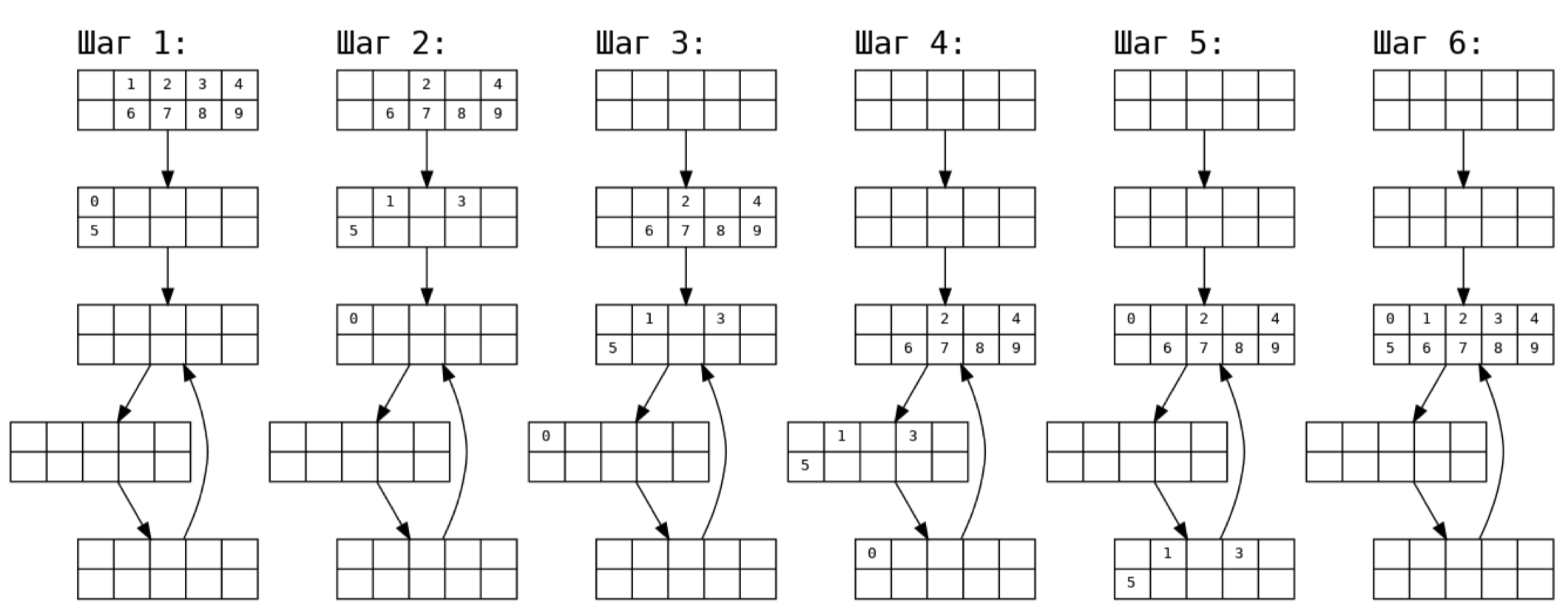
В примере перемещение друзей происходит следующим образом:
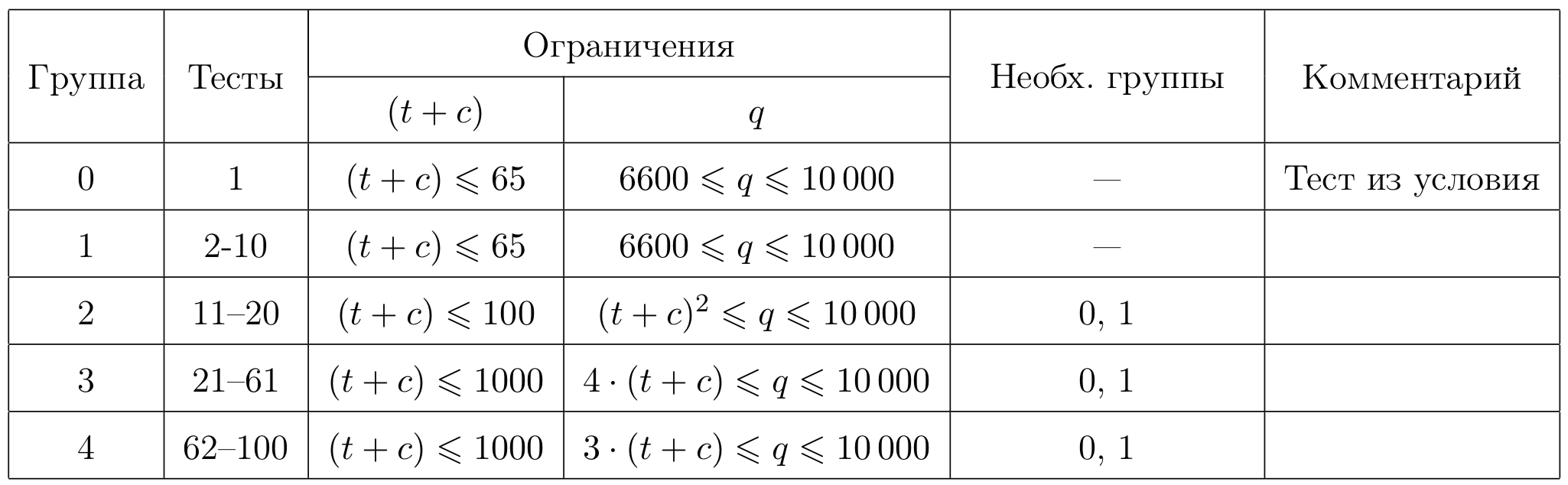
Тесты к этой задаче состоят из четырёх групп. Каждая группа тестируется только при прохождении всех тестов необходимых групп. В каждой тестируемой групе ваша программа будет запущена на всех тестах, каждый пройденный тест будет оценен в \(1\) балл. Группа считается пройденной только при прохождении всех тестов в ней.
2 3 10000
next 0 5 2 05 12346789 next 0 1 3 3 246789 135 0 next 2 3 0 1 4 5 6 7 8 9 3 246789 0 135 next 9 8 7 6 5 4 3 2 1 0 3 246789 0 135 next 0 1 3 5 2 135 0246789 next 1 3 5 1 0123456789 done