Задача №114122. Выбор вагона
Вася любит ездить на поездах, но не любит, когда вагон, в котором он едет, расположен в хвосте.
Вася садится на поезд на вокзале. Поезд состоит из \(n\) вагонов, пронумерованных от \(1\) до \(n\), считая от локомотива. Во время движения поезда происходит три типа событий:
- К голове поезда подцепляют некоторое количество вагонов;
- К хвосту поезда подцепляют некоторое количество вагонов;
- Вася пересчитывает величину, с помощью которой он оценивает удобство вагона (подробнее о ней ниже).
В каждый момент времени будем нумеровать вагоны начиная с головы поезда, начиная с \(1\). При добавлении новых вагонов к голове поезда, нумерация старых может сдвинуться.
Чтобы выбрать, в каком вагоне ехать, Вася ввёл для каждого вагона величину \(A_i\) (где \(i\) — номер вагона), которая вычисляется следующим образом:
- В начале поездки \(A_i=0\), а также для новых вагонов, в момент их добавления.
- Во время очередного пересчёта Вася выбирает целые положительные числа \(b\) и \(s\) и прибавляет к \(A_i\) величину \(b + (i - 1) \cdot s\).
Вася ещё не решил, откуда и куда ехать, поэтому после каждого события одного из трёх типов он хочет знать номер наиболее близкого к голове поезда вагона, что его значение \(A_i\) минимально. Так как вагонов очень много Вася попросил Вас написать программу, отвечающую на его вопрос.
Первая строка содержит два целых числа \(n\) и \(m\) (\(1 \leq n \leq 10^9\), \(1 \leq m \leq 300\,000\)) — количество вагонов в поезде на момент отправления с вокзала и количество станций соответственно.
Следующие \(m\) строк задают описания событий. Каждое событие одного из трёх следующих видов:
- «\(1\) \(k\)» (\(1 \le k \le 10^9\)), нужно подцепить к голове поезда \(k\) вагонов.
- «\(2\) \(k\)» (\(1 \le k \le 10^9\)), нужно подцепить к хвосту поезда \(k\) вагонов.
- «\(3\) \(b\) \(s\)» (\(1 \le b, s \le 10^9\)), нужно пересчитать удобство всех вагонов поезда.
Гарантируется, что в любой момент времени времени длина поезда не превышает \(10^9\), а все числа \(A_i\) не превышают \(10^{18}\).
После каждого из \(m\) запросов выведите два целых числа: \(j\) и \(A_j\) — номер наиболее близкого к голове поезда вагона, что его значение \(A_j\) минимально, и само значение \(A_j\).
-
Изначально поезд состоит из одного вагона \(A_1 = 0\), обозначим для простоты его как \([0]\).
-
После прицепления одного вагона к голове, получается поезд \([0, 0]\).
-
После уточнения с параметрами \(b=1, s=1\), получается поезд \([1, 2]\).
-
После ещё одного уточнения с параметрами \(b=1, s=1\), получается поезд \([2, 4]\).
-
После подцепления одного вагона в конец, получается поезд \([2, 4, 0]\).
-
После ещё одного подцепления одного вагона в конец, получается поезд \([2, 4, 0, 0]\).
-
После уточнения с параметрами \(b=1\), \(s=1\), получается поезд \([3, 6, 3, 4]\).
-
После подцепления одного вагона в конец, получается поезд \([3, 6, 3, 4, 0]\).
- После уточнения с параметрами \(b=1\), \(s=5\), получается поезд \([4, 12, 14, 20, 21]\).
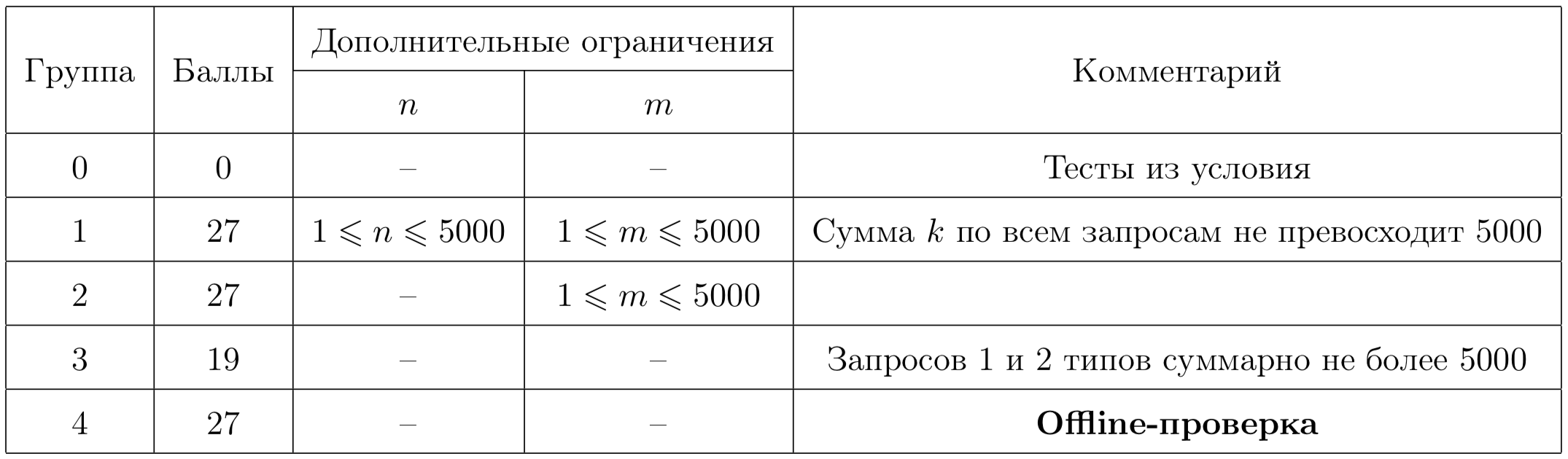
Тесты к этой задаче состоят из четырёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
1 8 1 1 3 1 1 3 1 1 2 1 2 1 3 1 1 2 1 3 1 5
1 0 1 1 1 2 3 0 3 0 1 3 5 0 1 4