Задача №114130. Классные парты
Для нового кабинета школы Иннополиса требуется купить \(n\) двухместных парт.
Парты бывают \(k\) типов, которые задают их размер. Парта типа \(i\) подходит школьникам, рост которых находится в диапазоне от \(L_i\) до \(R_i\) включительно. Остальным школьникам сидеть за такой партой неудобно, при этом величиной неудобства школьника, если он сидит за такой партой, будем называть модуль разности его роста и ближайшей границы диапазона этой парты. Если парта школьнику подходит, то для него величина неудобства равна нулю.
Например, если \(L_i = 100\) и \(R_i = 120\), то неудобство для школьника с ростом \(80\) равно \(20\), для школьника с ростом \(130\) равно \(10\), а для школьника с ростом \(105\) равно \(0\).
В кабинете по очереди будут заниматься \(m\) групп школьников, каждая из которых состоит из \(2n\) человек. Известен рост каждого школьника в каждой из групп. Закупленные парты будут расставлены в классе, и в каждой группе за каждой партой будут сидеть ровно два школьника. Необходимо купить \(n\) парт и рассадить за ними школьников каждой группы таким образом, чтобы суммарное неудобство для всех школьников, занимающихся в этом кабинете, было минимальным.
Требуется написать программу, которая по информации о каждом из \(k\) типов парт и известным значениям роста каждого школьника в каждой группе определяет, какого минимального суммарного значения неудобства школьников можно достичь, купив парты и рассадив за них школьников в каждой группе оптимальным образом.
В первой строке входных данных находятся три целых числа \(m\), \(n\) и \(k\) (\(1 \le m, n \le 200\,000\); \(1 \le m \cdot n \le 200\,000\); \(2 \leq k \leq 200\,000\)) — количество групп школьников, которые будут заниматься в кабинете, количество парт, которые необходимо купить, и количество типов парт соответственно.
В каждой из следующих \(k\) строк находятся по два целых числа \(L_i\) и \(R_i\) (\(1 \leq L_i \leq R_i \leq 10^9\)), характеризующие диапазон роста школьников, для которых подходят парты типа \(i\).
В каждой из следующих \(m\) строк находится описание группы. Каждое описание состоит из \(2n\) целых чисел \(h_1, h_2, \ldots, h_{2n}\), задающих значение роста каждого из \(2n\) школьников группы (\(1 \leq h_i \leq 10^9\)).
В единственной строке выходных данных выведите \(P\) — минимальную величину суммарного неудобства, которую можно достичь при оптимальной покупке парт.
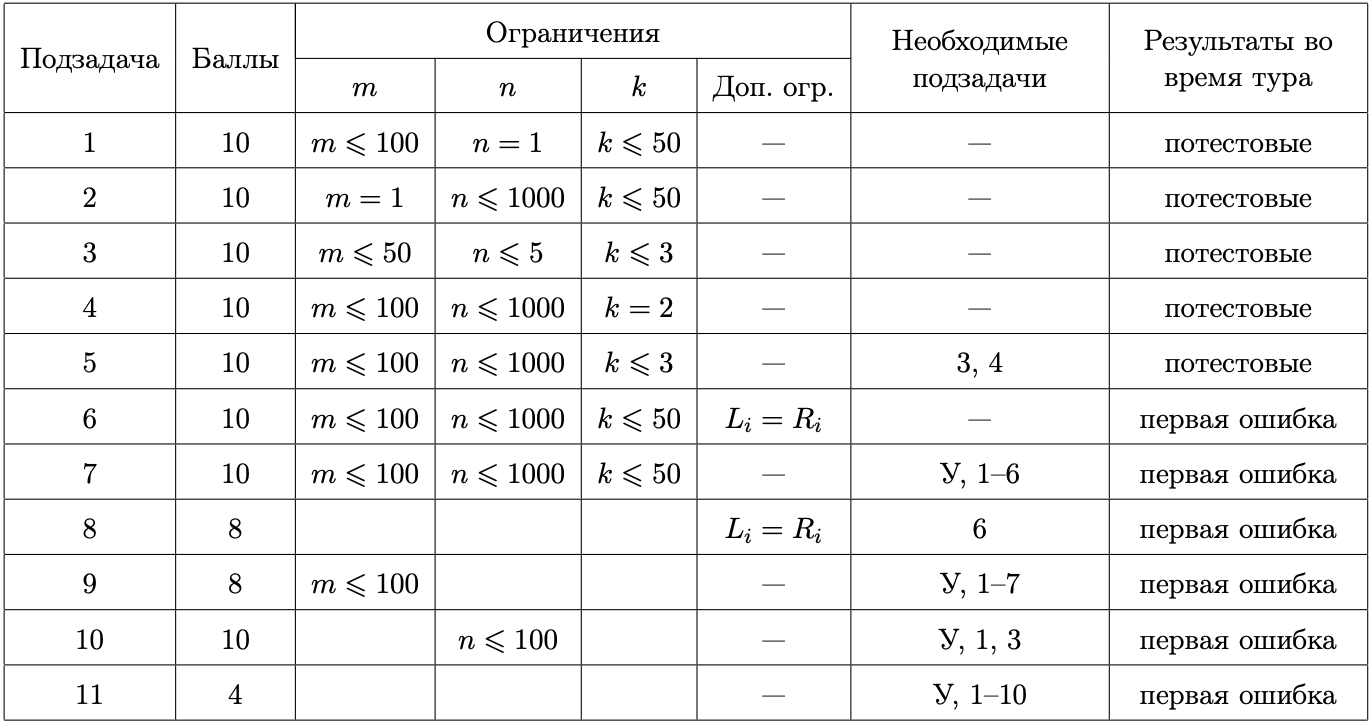
1 2 2 5 25 50 90 60 5 10 40
10
2 3 3 200 400 300 500 100 600 300 330 440 40 30 300 150 250 350 450 550 300
130
1 3 4 10 100 200 200 10 100 300 1000 5 10 20 15 200 90
105