Задача №114137. Флаг
Иннокентий работает на блошином рынке, продавая посетителям всякий хлам необычные вещи. Недавно он нашёл у себя на складе старое прямоугольное покрывало. Как оказалось, это покрывало имеет сетчатую форму, то есть покрывало состоит из \(n \cdot m\) цветных лоскутков, разбитых на \(n\) строк и \(m\) столбцов.
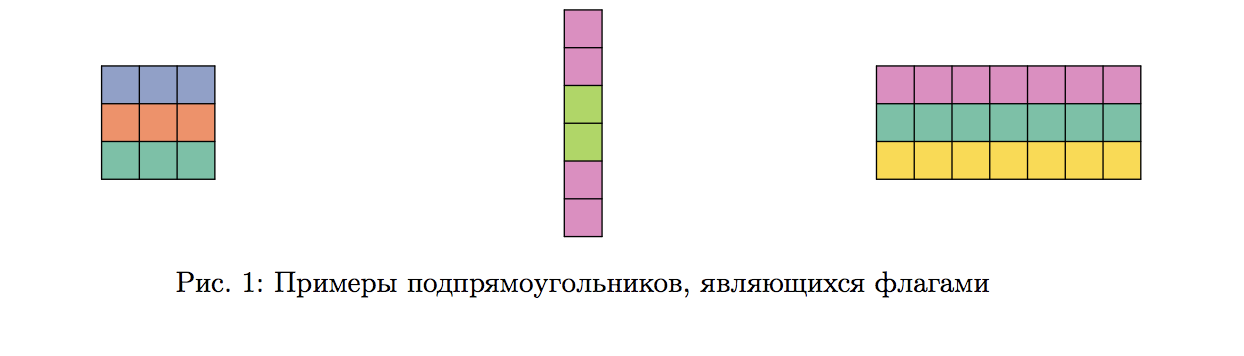
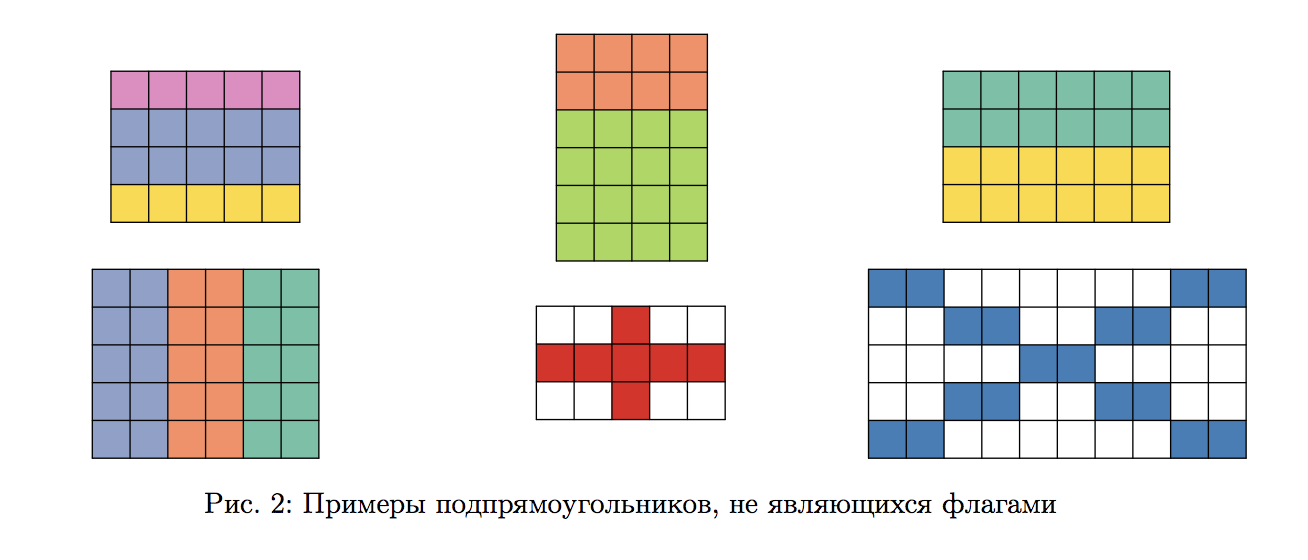
Цветные лоскутки привлекли внимание Иннокентия, и он сразу же придумал, как можно заработать на своей находке. Если вырезать из покрывала подпрямоугольник, состоящий из трёх цветных полос, то потом этот подпрямоугольник можно будет продать как флаг какой-нибудь страны. В частности, Иннокентий считает, что подпрямоугольник будет достаточно похож на флаг какой-нибудь страны, если он будет состоять из трёх одноцветных полос одинаковой высоты, находящихся друг под другом. Разумеется, цвет верхней полосы не должен совпадать с цветом средней полосы, а цвет средней не должен совпадать с цветом нижней.
Иннокентий пока не знает из какой части покрывала будет вырезать флаг, однако он точно решил, что будет вырезать флаг только по линиям сетки, при этом покрывало ни в коем случае нельзя поворачивать. Помогите Иннокентию и посчитайте количество различных подпрямоугольников, которые можно вырезать из покрывала и продать как флаг. Подпрямоугольники, образующие одинаковые флаги, однако расположенные в разных местах покрывала, считаются различными.
Первая строка содержит два целых числа \(n\) и \(m\) (\(1 \le n, m \le 1\,000\)) — количество строк и столбцов в покрывале.
Каждая из следующих \(n\) строк описывает очередную строку покрывала и состоит из \(m\) строчных латинских букв от « a » до « z », где одинаковым цветам соответствуют одинаковые буквы, а разным цветам — разные буквы.
В единственной строке выведите одно целое число — количество подпрямоугольников, являющихся флагами.
Данная задача состоит из \(20\) тестов, помимо теста из условия. Каждый из них оценивается в \(5\) баллов. Результаты проверки ваших решений на всех тестах будут доступны сразу во время соревнования.
-
Решения, корректно работающие при \(n, m \le 10\) наберут не менее \(20\) баллов.
-
Решения, корректно работающие при \(n, m \leq 100\), наберут не менее \(40\) баллов.
-
Решения, корректно работающие при \(n, m \leq 400\), наберут не менее \(65\) баллов.
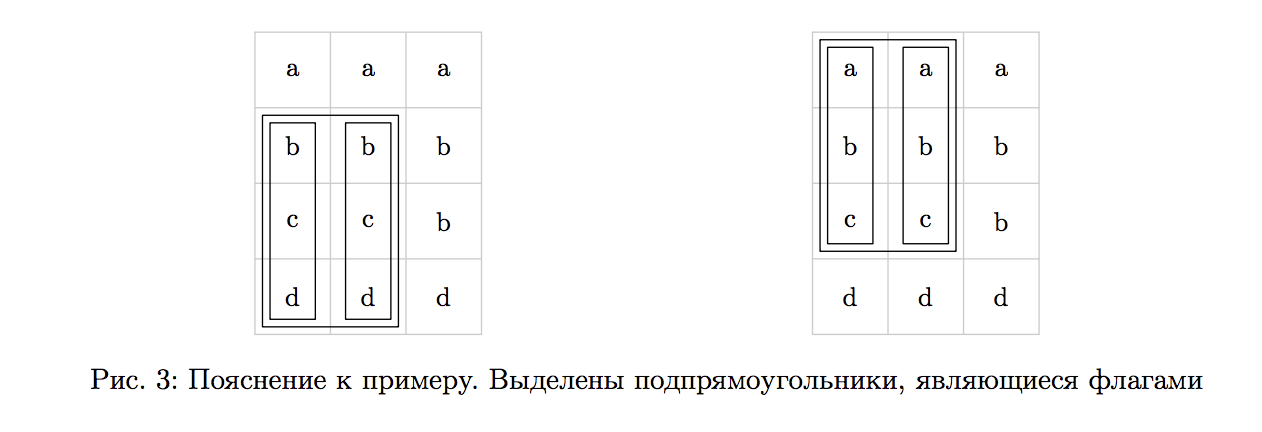
4 3 aaa bbb ccb ddd
6