Задача №114143. Иван Васильевич ищет прогрессию
На уроке Марья Ивановна дала классу следующую интересную задачу: на доске выписаны в порядке возрастания все целые числа от a до b включительно. Чему равна максимальная длина подпоследовательности данной последовательности, являющейся геометрической прогрессией?
Например, если на доске выписаны числа от
1
до
10
, то можно выбрать прогрессию из
4
элементов со знаменателем
q
= 2
, для этого требуется взять элементы
1
,
2
,
4
и
8
. Обратите внимание, что в отличие от элементов прогрессии знаменатель может не быть целым числом. Например, если Марья Ивановна выписывает все числа от
10
до
30
включительно, то, взяв в качестве знаменателя
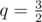 , можно получить прогрессию
12
,
18
,
27
.
, можно получить прогрессию
12
,
18
,
27
.
Обычно Иван Васильевич списывает все задания у своего друга Вильяма, но сегодня тот заболел и не пришёл, оставив Ивана Васильевича самостоятельно разбираться с поставленной задачей. Может хотя бы вы поможете ему в этом?
В первой строке входных данных записаны два целых числа a и b ( 1 ≤ a ≤ b ≤ 10 12 ).
Выведите одно целое число — максимально возможную длину подпоследовательности, являющейся геометрической прогрессией.
Последовательность чисел b 0 , b 1 , ..., b n является геометрической прогрессией со знаменателем q , если для всех i > 0 верно, что b i = b i - 1 · q . Как правило полагают b 0 ≠ 0 и q ≠ 0 , но в данной задаче это не имеет значения. Обратите внимание, что последовательность может состоять и из одного элемента.
В первом примере оптимально выбрать числа 1 , 2 , 4 и 8 .
Во втором примере оптимальную подпоследовательностью образуют числа 12 , 18 и 27 .
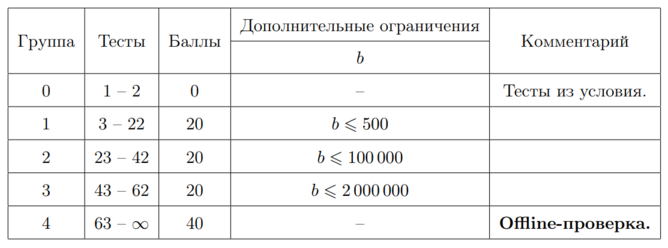
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
1 10
4
10 30
3