Задача №114144. Новые приключения Искандера и Оли
Искандер и Оля очень любят придумывать ребусы. Ещё Оля и Искандер очень любят по вечерам пить чай с тортиком. Поэтому они каждый день заходят в магазин неподалёку и покупают там вкусный торт с вишенками и печеньками.
Друзья очень ответственно подходят к выбору тортика и уже запланировали, какие именно тортики они хотят в ближайшие n дней. Искандер хочет, чтобы в день i на тортике было не менее a i и не более b i вишенок. Оля же хочет, чтобы в день i на тортике было не менее c i и не более d i печенек. Других требований к тортику у Оли и Искандера нет, в частности Искандеру не важно количество печенек, а Олю не волнует количество вишенок на торте. Поскольку ребята очень дружны, то в день i они купят тортик, если он понравится хотя бы одному из них .
Вы — владелец магазина тортиков и планируете в ближайшие n дней выпускать один и тот же тортик, то есть не менять количество вишенок и количество печенек. Ваша задача — найти такие значения для количества вишенок и количества печенек на тортике, чтобы Оля и Искандер купили его у вас в как можно большее число дней.
В первой строке входного файла содержится единственное число n ( 1 ≤ n ≤ 200 000 ) — число дней, на которое Оля и Искандер уже построили планы.
В следующих n строках находятся четверки целых неотрицательных чисел a i , b i , c i , d i — пожелания друзей. Все эти числа не превосходят 10 9 .
Выведите два неотрицательных целых числа p , q — количество вишенок и печенек на торте в любом из оптимальных решений. Выведенные вами числа не должны превосходить 10 9 .
В первом примере ребята купят тортик в дни 1 , 2 , 4 и 5 , то есть величина ответа равна 4 .
Во втором примере ребята построили планы только на один день, и вы легко сможете им угодить.
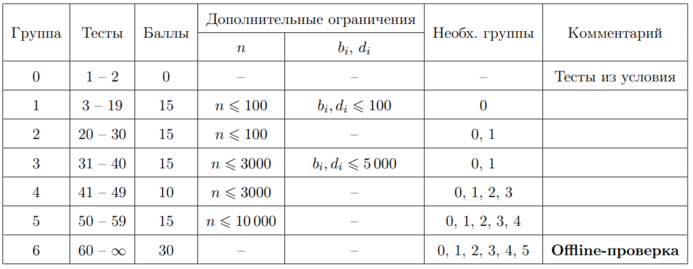
Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп, указанных в таблице ниже. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
5 2 3 1 2 3 5 1 2 7 8 8 9 5 6 2 3 3 5 6 8
5 1
1 0 10 0 10
1000000000 0