Задача №114145. Железная дорога
Железнодорожная сеть в одной стране состоит из n станций и некоторого количества однонаправленных дорог, их соединяющих. Некоторые дороги имеют переключатели, которые позволяют изменять один из концов дороги. А именно, для каждой дороги известно, на какой станции она начинается и на каких станциях может заканчиваться. При этом для позиций возможных концов фиксирован некоторый порядок, и активация переключателя для данной дороги меняет положение на следующее.
У железной дороги есть два директора: исполнительный и генеральный. Генеральному директору поручено управление вагонами, исполнительному — переключение дорог. На станцию s прибыл вагон с ресурсами. Нужно переместить этот вагон на станцию t за минимально возможное количество ходов. Каждый ход выглядит следующим образом:
- Сначала действует исполнительный директор. Он может не более одного раза активировать переключатель, изменив положение одной из дорог на следующее. Исполнительный директор может ничего не делать на своём ходу.
- Далее генеральный директор может не более одного раза использовать какую-либо дорогу, начинающуюся в станции, где сейчас расположен вагон, и передвинуть его в конец данной дороги. Генеральный директор также может ничего не делать на своём ходу.
Заметим, что в течение одного хода исполнительный директор может переключить некоторую дорогу, по которой на этом же ходу проедет вагон. Вам нужно помочь директорам и определить, за какое минимальное количество ходов они могут достичь желаемого.
В первой строке входных данных содержатся два числа n и m ( 2 ≤ n ≤ 400 , 1 ≤ m ≤ n ( n - 1) ) — количество станций и количество всех возможных состояний дорог.
Во второй строке записаны числа s и t ( 1 ≤ s , t ≤ n , s ≠ t ) — номер станции, на которой вагон находится изначально, и номер станции на которой он должен оказаться.
Далее следует информация о дорогах. Каждая строка даёт описание одной дороги и всех её состояний. В i -й из них записаны числа u i и k i ( 1 ≤ u i ≤ n , 1 ≤ k i ≤ n - 1 ), за которыми следуют k i различных чисел v i , 1 , ..., v i , k i ( 1 ≤ v i , 1 , ..., v i , k i ≤ n , u i ≠ v i , j ). Это означает, что в начальный момент времени дорога направлена от станции u i к станции v i , 1 , а одно применение переключателя переводит второй её конец из положения v i , j в положение v i , j + 1 (для j < k i ). Применение переключателя в положении v i , k i переставляет конец дороги в станцию v i , 1 .
Гарантируется, что
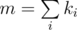. Также гарантируется, что существует последовательность действий, после выполнения которой вагон окажется на станции
t
.
В единственной строке выведите ответ на задачу: минимальное необходимое количество ходов для перемещения вагона. Гарантируется, что существует последовательность действий, позволяющая добиться этой цели.
В первом тесте из условия на первом ходу исполнительный директор занимается переключением дороги (1, 2) в состояние (1, 3) , а затем (всё в тот же первый ход) генеральный директор по ней передвигается.
Во втором тесте на первом ходу исполнительный меняет дорогу (2, 3) на дорогу (2, 4) , а генеральный директор продвигает вагон ко второй станции. Тогда на втором ходу вагон проезжает по последней дороге, достигая цели (исполнительный директор ничего не делает в свою фазу второго хода).
В третьем тесте существует два оптимальных способа добраться от станции
6
до станции
5
. Во-первых, исполнительный директор может ничего не делать всё время, и генеральный директор проведёт вагон по маршруту
, что займёт три хода. Во-вторых, можно действовать так: за первый ход дорога
(2, 4)
переключается в
(2, 3)
, вагон переезжает на первую станцию. К концу второго хода дорога
(2, 3)
переключается в состояние
(2, 5)
, а вагон оказывается на станции номер
2
. Наконец, в последний ход вагон перегоняется на конечную станцию. Исполнительный директор отдыхает начиная со третьего хода.
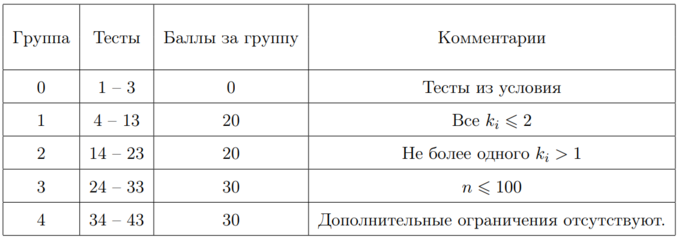
Тесты к этой задаче состоят из пяти групп. Группы 1, 2 и 3 не зависимы друг от друга, чтобы получить за них баллы, требуется пройти все тесты в группе. Чтобы получить баллы за группу 4 требуется пройти все тесты всех групп. Обратите внимание, в данной задаче ваше решение не обязано проходить тесты из условия, чтобы быть принятым на проверку на последующих группах.
3 2 1 3 1 2 2 3
1
4 4 1 4 1 1 2 2 2 3 4 3 1 4
2
8 8 6 5 6 1 7 6 1 1 7 1 8 1 1 2 8 1 5 2 3 4 3 5
3