Задача №114188. Турнир
В турнире участвуют \(N\) команд. Турнир проводится по олимпийской системе (команды играют на вылет, проигравшие команды выбывают из турнира, выигравшие проходят в следующий тур, ничьих не бывает). Число команд в этой задаче будет степенью двойки: \(N = 2^k\).
Все команды пронумерованы числами от 1 до \(N\). В первом туре играют команды с номерами 1 и 2, 3 и 4, 5 и 6 и т.д., всего играется \(N/2\) матчей. По результатам этих матчей команды выходят во второй тур. Во втором туре играют победители первой и второй игры первого тура, победители третьей и четвёртой игры первого тура и т.д. Они выходят в третий тур. В третьем туре играют вместе победители первой и второй игры второго тура, победители третьей и четвёртой игры второго тура и т.д.
Вам даны результаты всех матчей. Определите номер команды, которая стала победителем турнира.
В первой строке входных данных записано число \(N\) – количество команд,участвовавших в турнире. Оно является степенью двойки и может принимать значения от \(2^0 = 1\) до \(2^{16} = 65536\). Следующие \(N−1\) строк содержат результаты всех сыгранных матчей.Первые \(N / 2\) строк из них являются результатами матчей первого тура, затем идёт \(N/4\) строк с результатами второго тура, \(N/8\) строк с результатами третьего тура и т.д.
Результат каждого матча является одним из двух возможных чисел: 1 или 2. Число 1 означает, что в матче выиграла первая команда (номер которой меньше), число 2 означает, что в матче выиграла вторая команда (номер которой больше).
Программа должна вывести одно число – номер победившей в турнире команды.
Далее нарисована схема турнира для примера из условия.
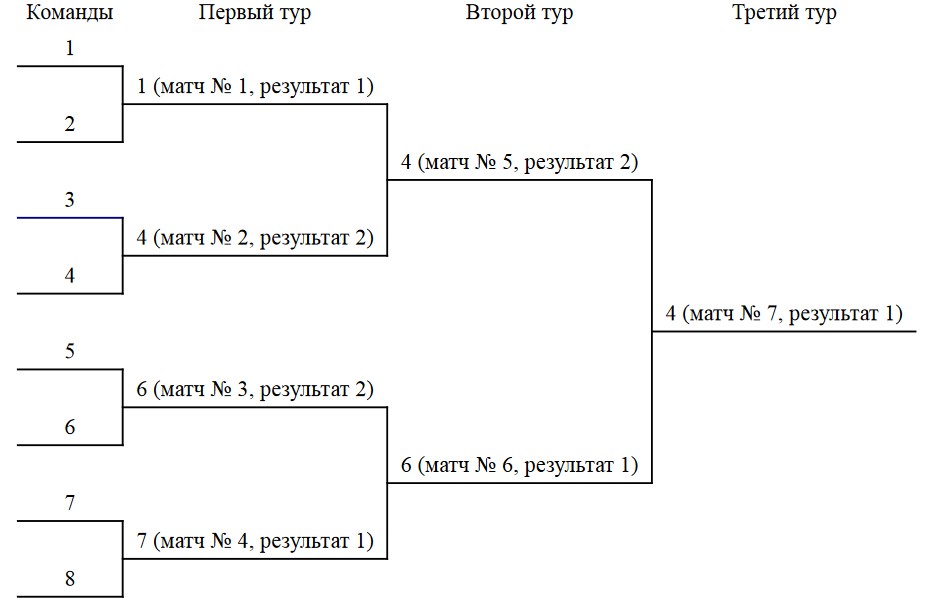
В турнире участвовало 8 команд. Результаты матчей: 1, 2, 2, 1, 2, 1, 1. В первом туре играли команды 1 и 2, 3 и 4, 5 и 6, 7 и 8. Результаты матчей первоготура: 1, 2, 2, 1, во второй тур вышли команды 1, 4, 6, 7.Во втором туре играли команды 1 и 4, 6 и 7. Результаты матчей второго тура: 2, 1.Втретий тур вышли команды 4 и 6. В последнем, третьем, туре играют команды 4 и 6, результат матча: 1, поэтому победителем турнира является команда 4.
Решение, правильно работающее только для случаев, когда \(N≤4\), будет оцениваться в 20 баллов.
Решение, правильно работающее только для случаев, когда \(N≤8\), будет оцениваться в 40 баллов.
8 1 2 2 1 2 1 1
4