Задача №114195. Танец
Для исполнения большого танца в круг выстроилось \(N\) танцоров (\(N\) чётное). Пронумеруем танцоров числами от \(1\) до \(N\) начиная от подиума по часовой стрелке. На каждом шаге танца танцоры разбиваются на пары (пару образуют два соседних по кругу танцора), и танцоры в паре меняются местам, причём на первом и всех последующих нечётных шагах танцор, стоящий в начале круга, образует пару с танцором, стоящим рядом с ним по часовой стрелке. Также пару образуют два танцора, следующие за ними по часовой стрелке, и т. д. На втором шаге и всех шагах с чётными номерами танцор, стоящий в начале круга, образует пару с танцором, стоящим рядом с ним против часовой стрелки. Два танцора, следующие за ними против часовой стрелки, также образуют пару и т. д.
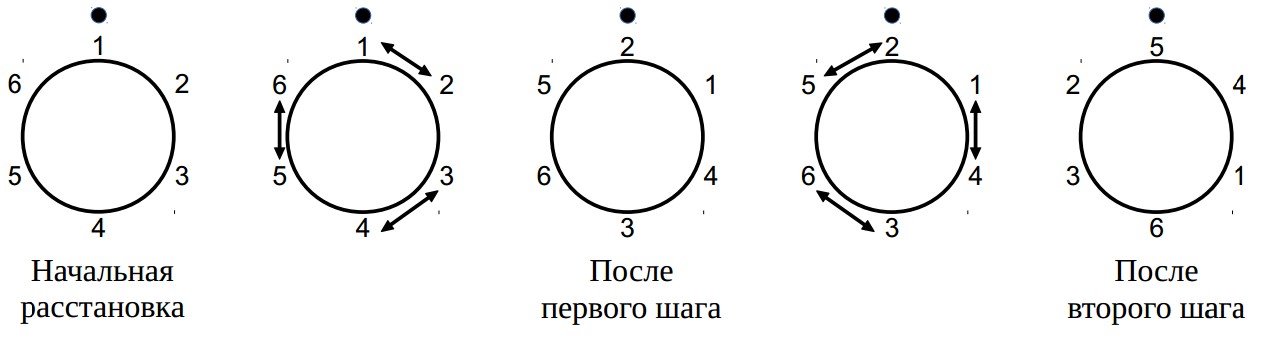
На рисунке изображена начальная расстановка для \(N = 6\) танцоров и два следующих шага танца. Расположение подиума отмечено точкой.
Определите, кто будет стоять рядом с танцором номер \(P\) через \(K\) шагов.
Программа получает на вход три целых числа \(N, P, K\), записанные в отдельных строках. Первое число \(N\) – количество танцоров в кругу, \(N\) чётное. Второе число \(P\) – номер танцора, \(1 ≤ P ≤ N\). Третье число \(K\) – количество сделанных шагов после начала танца, \(1 ≤ K\). Максимальные значения для \(N\) и \(K\) приведены в разделе «Система оценивания».
Программа должна вывести два целых числа в порядке возрастания – номера танцоров, которые будут стоять рядом с танцором номер \(P\) после \(K\) шагов танца.
Каждый тест к этой задаче (кроме теста из условия) оценивается в 5 баллов. В таблице приведены ограничения на \(N\) и \(K\) для всех тестов.
| Номера тестов | Количество баллов за все тесты группы | Ограничение на \(N\) и \(K\) |
| 1 0 | 0 | Пример из условия |
| 2–7 | 30 | \(N ≤ 100, K ≤ 100\) |
| 8–9 | 10 | \(N ≤ 100, K ≤ 10^9\) |
| 10–13 | 20 | \(N ≤ 10^5, K ≤ 10^5\) |
| 14–15 | 10 | \(N ≤ 10^5, K ≤ 10^9\) |
| 16–21 | 30 | \(N ≤ 10^9, K ≤ 10^9\) |
6 5 2
2 4