Задача №1142. Произведения
 Петя участвует в конкурсе юных любителей головоломок. В последнем туре участникам предложена следующая задача:
Петя участвует в конкурсе юных любителей головоломок. В последнем туре участникам предложена следующая задача:
Дана квадратная таблица N на N. Рядом с каждым столбцом и каждой строкой написано целое положительное число. Пусть около i-го столбца написано число Xi, а около j-й строки – число Yj. Для победы в конкурсе необходимо в некоторых клетках таблицы расположить целые положительные числа так, чтобы выполнялись следующие условия:
- Все эти числа должны быть различными
- В каждом столбце и каждой строке должно быть ровно 2 числа
- Произведение чисел i-го столбца должно быть равно Xi.
- Произведение чисел j-й строки должно быть равно Yj.
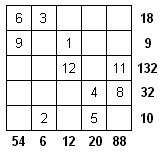
Рисунок показывает пример решения такой задачи.
Помогите Пете!
На первой строке входного файла находится число N (2 ≤ N ≤ 10). На второй строке находится N чисел - X1...XN (1 ≤ Xi ≤ 1000 для всех 1 ≤ i ≤ N). На третьей строке также находится N чисел - Y1...YN (1 ≤ Yi ≤ 1000 для всех 1 ≤ i ≤ N).
Выведите в выходной файл таблицу после расстановки в ней чисел необходимым образом. Таблицу следует выводить по строкам: сначала N чисел первой строки, затем N чисел второй строки, и т. д. Если в соответствующей клетке стоит число, следует вывести это число, если клетка осталась пустой, следует вывести 0. Все числа в выходном файле следует разделять пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если решений несколько, выведите любое из них. Гарантируется, что хотя бы одно решение будет существовать.
2 15 8 6 20
3 2 5 4
3 3 10 24 2 12 30
1 2 0 3 0 4 0 5 6