Задача №114202. Площадь
Городская площадь имеет размер \(n х m\) и покрыта квадратной плиткой размером \(1 х 1\). При плановой замене плитки выяснилось, что новой плитки недостаточно для покрытия всей площади, поэтому было решено покрыть плиткой только дорожку по краю площади, а в центре площади разбить прямоугольную клумбу (см. рисунок к примеру). При этом дорожка должна иметь одинаковую ширину по всем сторонам площади. Определите максимальную ширину дорожки, которую можно выложить из имеющихся плиток.
Первая и вторая строки входных данных содержат по одному числу \(n\) и \(m\) \((3 \le n \le 2 х 10^9, 3 \le m \le 2 х 10^9)\) — размеры площади.
Третья строка содержит количество имеющихся плиток \(t, 1 \le t < nm\).
Обратите внимание, что значение \(t\) может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные числа (тип int64 в языке Pascal, тип long long в С и С++, тип long в Java и С#).
Программа должна вывести единственное число - максимальную ширину дорожки, которую можно выложить из имеющихся плиток.
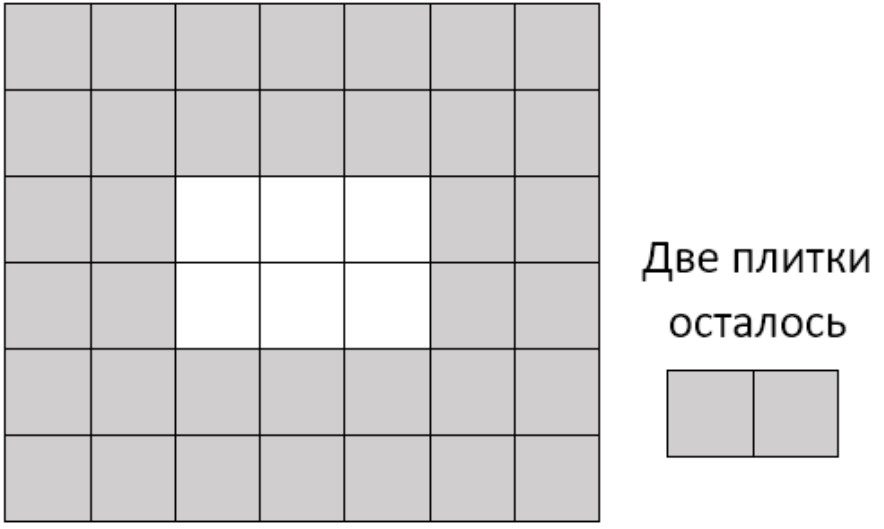
Пояснение к примеру. Площадь имеет размеры 6 х 7, из 38 плиток можно выложить дорожку шириной в 2 плитки.
Решение, правильно работающее только для случаев, когда числа \(п\) и \(m\) не превосходят 1000, будет оцениваться в 60 баллов.
6 7 38
2