Задача №114204. Космические шахматы
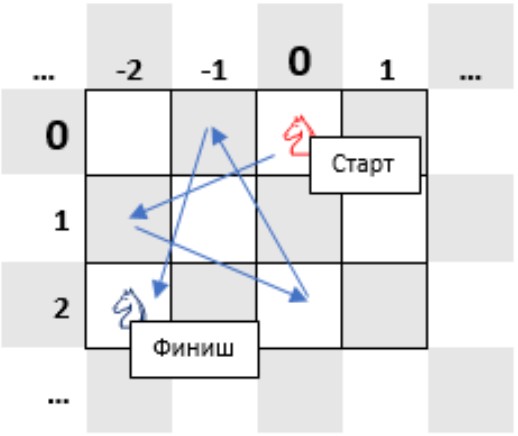
В космические шахматы играют на бесконечной доске, поэтому клетки нумеруют парой чисел (см. пример и рисунок к нему). Фигуры ходят по обычным правилам. Составьте маршрут шахматного коня из клетки \((0; 0)\) в заданную клетку \((x; y)\).
Напомним, что конь за один ход перемещается на одну клетку по одной оси и на две по другой, то есть, например, из клетки \((0; 0)\) он за один ход может попасть в клетки \((1; 2), (2; 1), (—1; 2), (2; — 1), (1; —2) (—2;1), (—1; —2)\) и \((—2; —1)\).
В качестве ответа Вам нужно вывести любой (не обязательно кратчайший) маршрут с началом в \((0; 0)\) и концом в \((x; y)\), длина которого не больше \(10^5\) ходов.
Программа получает на вход два целых числа \(x\) и \(y\), записанных в отдельных строках, — координаты конечной клетки маршрута коня. Клетка \((x; y)\) не совпадает с началом координат. \(|x| \le 10^5, |у| < 10^5\).
Программа должна вывести последовательность ходов, один ход в отдельной строке. В \(i\)-й строке должно быть выведено два числа \(x_i\) и \(у_i\) через пробел — координаты клетки, в которой окажется конь после \(i\)-ro хода. Количество ходов не должно превышать \(10^5\). Последний ход должен вести в заданную клетку.
Рисунок к примеру
Решение, правильно работающее только для случаев, когда \(|x| \le 1, |у| \le 1\), будет оцениваться в 16 баллов.
Решение, правильно работающее только для случаев, когда \(|x| \le 100, |у| \le 100\), будет оцениваться в 40 баллов.
Решение, правильно работающее только для случаев, когда \(|x| \le 15 000, |у| \le 15 000\), будет оцениваться в 70 баллов.
-2 2
-2 1 0 2 -1 0 -2 2