Задача №114550. Неклассические классики
Петя с Машей на перемене решили выйти во двор и поиграть в классики. К сожалению, ночью шел дождь, поэтому любимое поле ребят смыло с асфальта. Теперь им надо начертить поле для игры заново.
Наши герои играют в так называемые «Неклассические классики». Отличие этой игры от привычных нам классиков состоит в том, что поле для игры может иметь разные формы, а именно, выбираются числа \(a,\,b,\,n,\,k\). После этого создается поле, где в первой строке будет \(a\) квадратных клеток, во второй строке будет \(b\) квадратных клеток, в третьей строке снова \(a\) клеток, затем опять \(b\) клеток, и так далее... После того, как на поле окажется \(2 \cdot k\) строк, ребята нарисуют строку из \(n\) клеток, после чего поле будет готово для игры. Клеточки в каждой строке будут одного размера, а центры всех строк должны оказаться на одной оси.
Например, поле для стандартных классиков можно создать, если выбрать числа \(a=1,\ b=2,\ n=1,\ k = 3\). Тогда получится такое поле:

А если взять \(a=3,\ b=4,\ n=2,\ k=1\), то получится такое поле:
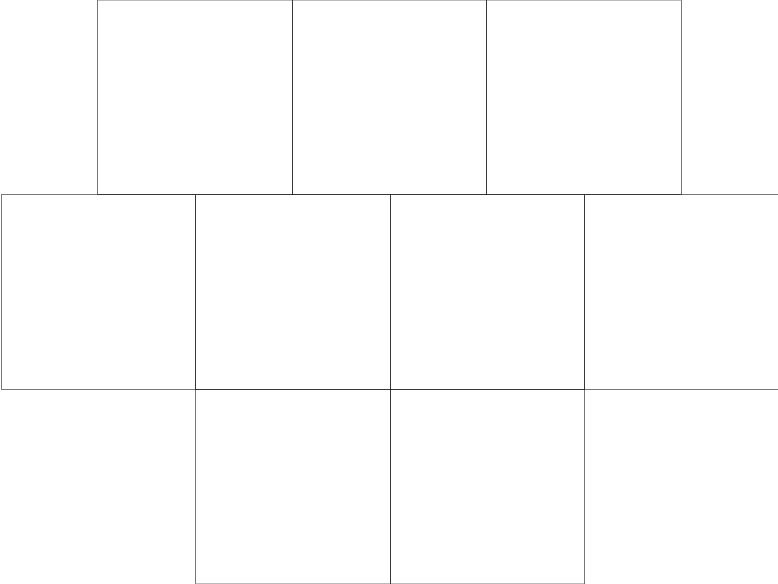
Петя с Машей рисуют поле следующим образом: с помощью двух камушков и веревочки Петя намечает прямую линию, а Маша проводит вдоль нее мелом отрезок. Будем считать, что длина Петиной веревочки не ограничена. Ребята несколько раз повторяют эту операцию, рисуя отрезки, пока не нарисуют все поле.
Петю заинтересовало, какое минимальное количество отрезков они могут нарисовать, чтобы получить требуемое поле. Маша не знала ответ на этот вопрос, и они обратились к вам. Помогите ей с решением этой задачи.
В первой строке задано целое число \(a\) (\(1 \le a \le 10^6\)) — количество клеток в строках с номерами \(1,\ 3,\ 5,\ \ldots,\ 2 \cdot k - 1\).
Во второй строке задано целое число \(b\) (\(1 \le b \le 10^6\)) — количество клеток в строках с номерами \(2,\ 4,\ 6,\ \ldots,\ 2 \cdot k\).
В третьей строке задано целое число \(n\) (\(1 \le n \le 10^6\)) — количество клеток в последней строке, имеющей номер \(2 \cdot k + 1\).
В четвертой строке задано целое число \(k\) (\(1 \le k \le 100\)) — количество повторений строк (то есть, количество раз, которое повторяются \(a\)-ряды и \(b\)-ряды).
Выведите одно целое число — минимальное количество отрезков, которое необходимо для того, чтобы нарисовать поле.
Рисунки полей для тестов из примеров приведены в условии.
Для поля из первого теста ребятам придется обвести всю фигуру, использовав 17 вертикальных отрезков одинаковой длины и 8 горизонтальных отрезков.
Поле из второго теста можно изобразить с помощью 4-х горизонтальных отрезков, а также 9-и вертикальных: из них 6 отрезков будут короткими, а еще 3 отрезка будут в два раза больше.
В данной задаче \(25\) тестов, помимо тестов из условия, каждый из них оценивается в \(4\) балла. Результаты работы ваших решений на всех тестах будут доступны сразу во время соревнования.
Решения, корректно работающие при \(1 \le a,\,b,\,n,\,k \le 10\), наберут не менее \(20\) баллов.
Решения, корректно работающие при \(a = b = n\), наберут не менее \(20\) баллов.
Решения, корректно работающие при \(a = b\), наберут не менее \(40\) баллов.
1 2 1 3
25
3 4 2 1
13