Задача №114637. Иванушка-дурачок и теория вероятностей
Недавно Иванушка-дурачок захотел стать умнее и поэтому начал изучать теорию вероятностей. Он считает, что уже достаточно хорошо понимает данную тему, и стал этим хвастаться перед всеми.
Чтобы не быть голословным, Иванушка пообещал продемонстрировать окружающим свои навыки при помощи случайного рисунка. Рисунок представляет собой клетчатое поле с \(n\) строками и \(m\) столбцами, каждая клетка которого покрашена в белый или чёрный цвет. Иванушка считает, что рисунок случайный, если для любой клетки верно, что среди ее соседей по стороне не более одной клетки такого же цвета, что и она.
Его братья быстро выяснили, что задумал Иванушка. Они долго пытались объяснить ему, что он, дурачок, все ещё плохо понимает, что такое случайность. Но Иванушка так и не поверил им, поэтому они попросили помощи у вас. Они хотят найти количество различных случайных по мнению Иванушки рисунков. Два рисунка называются различными если существует клетка, которая покрашена в разные цвета на этих рисунках. Так как это число может быть слишком большим, найдите остаток от деления его на \(10^9 + 7\).
В единственной строке заданы два целых числа \(n\) и \(m\) (\(1 \leq n, m \leq 100\,000\)) — количество строк и столбцов клетчатого поля, соответственно.
Выведите одно целое число — остаток от деления числа случайных рисунков на \(10^9 + 7\).
На картинке ниже изображены все возможные случайные раскраски поля \(2\) на \(3\).
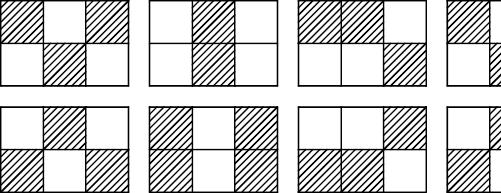
2 3
8