Задача №114694. Дед и мопед
Дед Максим собирается в путешествие по Флатландии. К сожалению, из доступных средств передвижения у него есть только мопед, запас хода которого ограничен. Более точно, если бак мопеда полностью заполнен, то мопед может проехать не более \(s\) километров без дополнительной дозаправки.
Всего во Флатландии есть \(n\) городов, пронумерованных от \(1\) до \(n\). В некоторых городах находятся заправки, и если в городе есть заправка, то в этом городе дед Максим может полностью наполнить бак. К сожалению, заправки присутствуют лишь в \(k\) городах. Также во Флатландии есть \(m\) дорог, \(i\)-я из которых соединяет города \(u_i\) и \(v_i\) и имеет длину \(c_i\) километров. По каждой дороге можно перемещаться в обоих направлениях.
Дед Максим начинает свое путешествие в городе с номером 1 с полным баком (в городе 1 есть заправка). Помогите ему определить, до каких городов он сможет добраться на мопеде.
В первой строке записаны четыре целых числа \(n,\,m,\,k,\,s\) (\(1 \le n \le 150\,000\), \(0 \le m \le 150\,000\), \(1 \le k \le n\), \(1 \le s \le 10^9\)) — количество городов, количество дорог, количество заправок и объем бака.
В следующих \(m\) строках записаны по три целых числа \(u_i, v_i, c_i\) (\(1 \le u_i,\,v_i \le n\), \(u_i \neq v_i\), \(1 \le c_i \le s\)) — начало, конец и длина \(i\)-й дороги. Гарантируется, что не существует двух дорог, соединяющих одинаковую пару городов.
В следующей строке записаны \(k\) целых чисел \(p_i\) (\(1 \le p_i \le n\)) — номера городов с заправками. Гарантируется, что заправка присутствует в городе 1.
В первой строке выведите единственное число \(x\): количество гордов, до которых дед Максим может добраться.
Во второй строке выведите \(x\) целых чисел — номера подходящих городов в порядке возрастания .
Рисунок ниже иллюстрирует первый пример из условия:
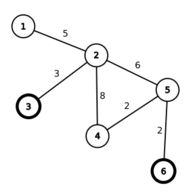
Из начального города с номером 1 можно доехать до городов с номерами 2 и 3 без дополнительных дозаправок. Также можно доехать до города с номером 3, пополнить там бак и доехать до города с номером 5. До городов 4 и 6 добраться невозможно, так как минимальное расстояние от достижимой заправки до них равно 11.
Тесты к этой задаче состоят из семи групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
| Доп. ограничения | ||||||
| Группа | Баллы | \(k\) | \(n\) | \(c_i\) | Необх. группы | Комментарий |
| 0 | 0 | – | – | – | – | Тесты из условия. |
| 1 | 15 | – | \(n \le 100\) | – | 0 | |
| 2 | 11 | \(k = 1\) | \(n \le 5000\) | – | – | |
| 3 | 8 | \(k = 1\) | – | – | 2 | |
| 4 | 12 | – | \(n \le 5000\) | \(c_i = 1\) | – | |
| 5 | 9 | – | \(n \le 5000\) | \(c_i \le 10\) | 0, 4 | |
| 6 | 17 | – | \(n \le 5000\) | – | 0, 1, 2, 4, 5 | |
| 7 | 28 | – | – | – | 0–6 | Offline-проверка. |
6 6 3 10 1 2 5 2 3 3 2 4 8 2 5 6 4 5 2 5 6 2 1 3 6
4 1 2 3 5