Задача №114838. Последняя битва
Близится решающий бой между марсианами и людьми. Шпионы людей выяснили, что у марсиан осталось n бойцов. Также выяснилось, что у людей, как и у марсиан, осталось ровно n бойцов.
По опыту прошлых сражений люди знают, что i -го человека может победить только один марсианин, который имеет номер i .
Командир решил выстроить людей в шеренгу. Узнав планы марсиан, командир выяснил, что человек с i -й позиции в шеренге будет сражаться с марсианином номер a i . Люди победят, только если каждый из бойцов гарантированно победит в своём бою.
Сначала командир поставил i -го человека на i -ю позицию в шеренге. После этого он понял, что у него осталось мало времени до битвы и люди могут проиграть, если оставить все как есть. За одну секунду он может переставить человека с последнего места в начало шеренги, после этой операции он оказывается на первой позиции, а номер позиции каждого из остальных бойцов увеличивается на 1 .
Помогите командиру понять, за какое минимальное время он сможет перестроить шеренгу так, чтобы люди победили в решающем бою.
В первой строке задано целое число n — количество бойцов у каждой из сторон ( 1 ≤ n ≤ 2·10 5 ).
Во второй строке задано n различных целых чисел a 1 , a 2 , ..., a n , где a i — номер марсианина, с которым будет сражаться человек на i -й позиции в шеренге ( 1 ≤ a i ≤ n , если i ≠ j , то a i ≠ a j ).
Выведите единственное число k — минимальное число секунд, за которое командир сможет перестроить шеренгу так, чтобы люди победили. Если победить марсиан невозможно, выведите число « - 1 ».
В первом примере исходно бойцы стоят друг напротив друга следующим образом:
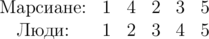
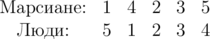
Теперь марсиане 2 и 3 выигрывают свой бой, поэтому необходимо провести ещё перестановку. После неё расстановка бойцов становится такой, что все люди выигрывают свой бой.
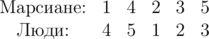
5 1 4 2 3 5
2
5 1 3 5 2 4
-1