Задача №115137. Печатная машинка

Участникам, использующим язык Python3 , рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3 .

Недавно Поликарпу подарили необычную печатную машинку!

Машинка состоит из $n$ ячеек, пронумерованных слева направо от $1$ до $n$, и движущейся над ними каретки. В ячейках печатной машинки лежат $n$ различных чисел от $1$ до $n$, причем в каждой ячейке $i$ изначально лежит число $p_i$. До всех действий каретка находится на ячейке с номером $1$ и в ее буферном хранилище ничего нет. Назовем ячейку текущей , если каретка стоит на этой ячейке.

Она может выполнять пять типов операций:

Взять число из текущей ячейки и положить его в буфер каретки, если текущая ячейка не пуста, а буфер пуст.
Положить число из буфера каретки в текущую ячейку, если она пустая.
Поменять местами число, которое находится в буфере каретки, с числом, которое находится в текущей ячейке, если и буфер, и ячейка содержат числа.
Сдвинуть каретку с текущей ячейки $i$ на ячейку $i + 1$ (если $i < n$), при этом число в буфере сохраняется.
Сбросить каретку, то есть переместить ее на ячейку с номером $1$, при этом число в буфере сохраняется.

Поликарпа очень заинтересовала эта печатная машинка, поэтому он просит вас помочь разобраться в ней и задаст вам $q$ запросов трех типов:

Выполнить циклический сдвиг последовательности $p$ на $k_j$ влево.
Выполнить циклический сдвиг последовательности $p$ на $k_j$ вправо.
Развернуть последовательность $p$.

До всех запросов, а также после каждого запроса Поликарп хочет узнать, сколько необходимо сбросов каретки для текущей последовательности, чтобы распределить числа по своим ячейкам (чтобы число $i$ оказалось в клетке с номером $i$).

Обратите внимание , что Поликарп хочет только узнать минимальное количество сбросов каретки для расположения чисел по своим местам, но он не распределяет их на самом деле.

Помогите Поликарпу узнать ответы на интересующие его запросы!

Входные данные

Первая строка содержит одно целое число $n$ ($1 \le n \le 200\,000$) — количество ячеек.

Вторая строка содержит $n$ целых различных чисел $p_1, p_2, \ldots, p_n$ ($1 \le p_i \le n$) — изначальное расположение чисел по ячейкам.

Третья строка содержит единственное число $q$ ($0 \le q \le 200\,000$) — количество запросов.

В каждой из следующих $q$ строках содержится запросы Поликарпа:

В строке $j$ сначала идет число $t_j$ – тип запроса ($1 \le t_j \le 3$).

Если запрос типа $t_j = 1$ или $t_j = 2$, то далее, в той же строке, содержится число $k_j$ — длина сдвига ($1 \le k_j \le n$).

Выходные данные

Выведите $q + 1$ число — минимальное количество сбросов каретки до всех запросов, а также после каждого запроса Поликарпа.

Примечание

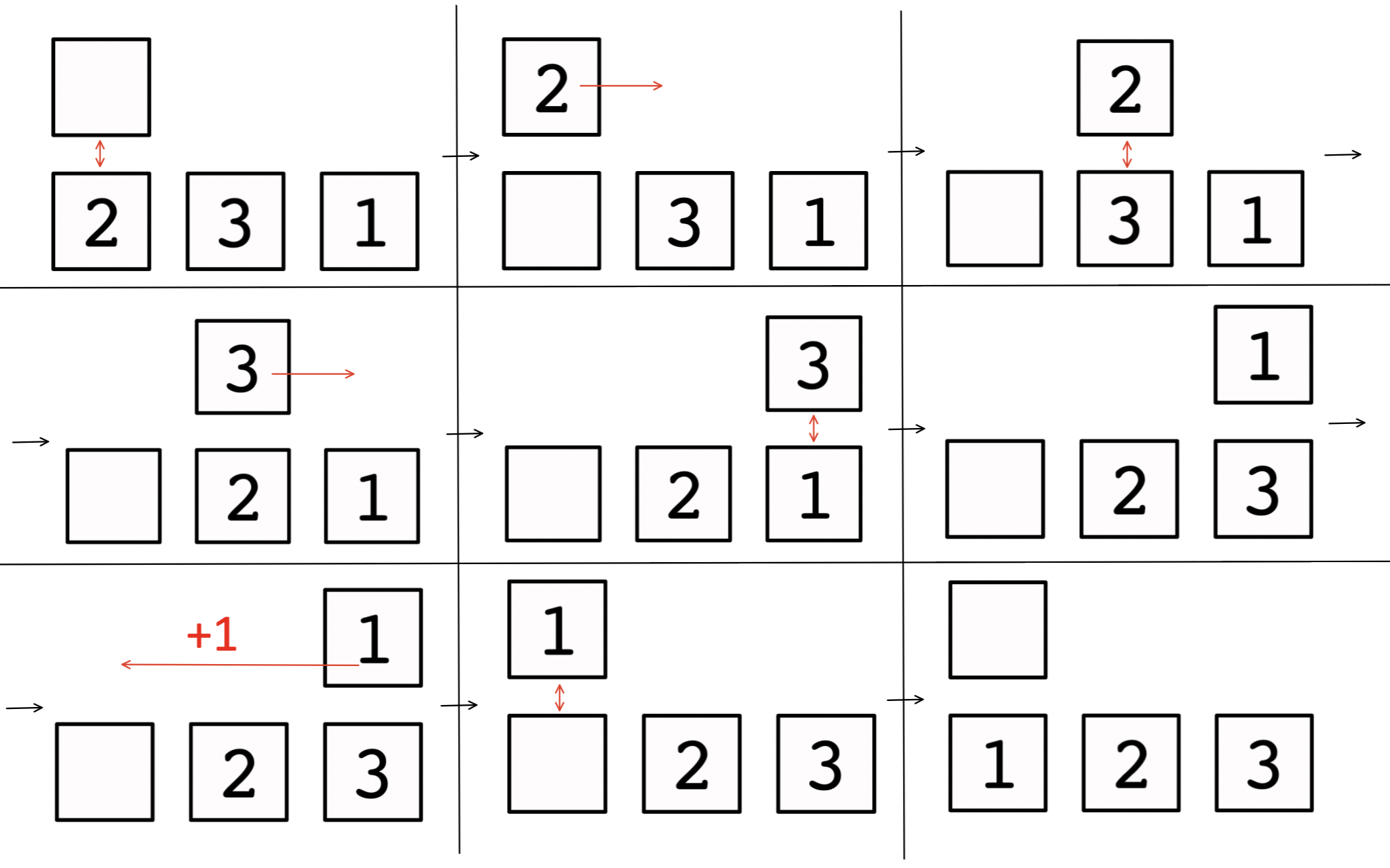
В первом примере ответ $1$. По рисунку ниже можно понять, как работает каретка в этом примере.

$\text{[math]}$

Во втором примере последовательности, для которых нужно посчитать ответ, выглядят так:

До всех запросов: $1\ 2\ 3$ — ответ $0$.
После сдвига на $1$ вправо: $3\ 1\ 2$ — ответ $2$.
После разворота последовательности: $2\ 1\ 3$ — ответ $1$.

В третьем примере последовательности до всех запросов и после каждого запроса выглядят так:

$3\ 1\ 2\ 5\ 4$ — ответ $3$.
$5\ 4\ 3\ 1\ 2$ — ответ $2$.
$2\ 1\ 3\ 4\ 5$ — ответ $1$.
$3\ 4\ 5\ 2\ 1$ — ответ $2$.
$1\ 3\ 4\ 5\ 2$ — ответ $1$.
$2\ 5\ 4\ 3\ 1$ — ответ $2$.

Система оценки

Тесты к этой задаче состоят из 5 групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп.

		Доп. ограничения
Группа	Баллы	$n$	$m$	Необх. группы	Комментарий
0	0	–	–	–	Тесты из условия.
1	16	$n \le 6$	$q = 0$	–
2	20	$n \le 2000$	$q \le 2000$	0, 1
3	17	–	–	–	Все $p_i = i$.
4	24	–	–	1	Нет запросов типа $t_j = 3$.
5	23	–	–	0–4

Примеры

Входные данные

3
2 3 1
0

Выходные данные

Входные данные

Выходные данные

0
2
1

Входные данные

Выходные данные

Сдать: для сдачи задач необходимо войти в систему