Задача №115153. Еж на дереве
Вам дано дерево из \(n\) вершин, причем \(i\)-я вершина имеет вес \(a_i\). Ежом называется связный подграф этого дерева с выделенной вершиной \(v\), такой что из \(v\) в разные стороны отходит несколько (хотя бы 2) путей равной длины (возможно нулевой).
Весом ежа называется сумма весов вершин, входящих в него.
Найдите вес самого тяжелого ежа на данном дереве.
В первой строке дано число \(n\) \((3 \le n \le 5 \cdot 10^5)\) — количество вершин в дереве.
Во второй строке дано \(n-1\) число \(p_2, p_3, \ldots, p_n\) \((1 \le p_i \le i - 1)\) — предки вершин \(2, 3, \dots n\).
В третьей строке даны \(n\) чисел \(a_1, a_2, \ldots, a_n\) \((-10^9 \le a_i \le 10^9)\) — веса вершин.
Выведите одно число — вес самого тяжелого ежа на данном дереве.
Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
В первом примере оптимальным ответом является набор вершин \(4, 5, 7\). Они образуют ежа с центром в вершине \(5\). Вес такого ежа равен \(a_4 + a_5 + a_7 = -1 + 5 + 4 = 8\).
Во втором примере самым тяжелым ежом является набор вершин \(1, 2, 3\). Обратите внимание, что нельзя составить ежа из вершин с номера \(1, 2\), потому что путей должно быть хотя бы два.
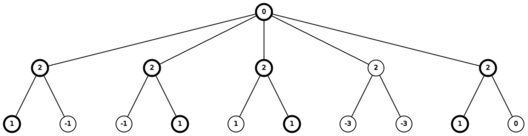
Ниже приведено дерево, которое дано в третьем примере. Жирными выделены вершины, образующие одного из оптимальных ежей:
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп.
| Ограничения | ||||
| Подз. | Баллы | \(n\) | дополнительно | Необх. подзадачи |
| 0 | 0 | – | – | Тесты из условия. |
| 1 | 15 | \(n \le 200\,000\) | \(p_i = i - 1\) | – |
| 2 | 15 | \(n \le 200\,000\) | \(a_i = 1\) | – |
| 3 | 15 | \(n \leq 2\,000\) | – | 0 |
| 4 | 15 | \(n \le 200\,000\) | степень любой вершины \(\le 4\) | 1 |
| 5 | 20 | \(n \le 200\,000\) | – | 0 – 4 |
| 6 | 20 | – | – | 0 – 5 |
8 1 1 3 4 3 5 1 -1 1 -2 -1 5 1 4 2
8
5 1 2 3 4 3 3 -1 -10 4
5
16 1 1 1 1 1 2 2 3 3 4 4 5 5 6 6 0 2 2 2 2 2 1 -1 -1 1 1 1 -3 -3 1 0
12