Задача №115159. Сериал по Майнкрафту
Маленький Миша ходит на кружок по программированию и ничего там не решает. Это может показаться странным, но когда вы узнаете, что Миша снимает сериал по Майнкрафту, все сразу встанет на свои места...
Миша, вдохновляясь застройкой Манхэттена, построил в Майнкрафте город, который можно представить в виде таблицы \(n \times m\). В городе живут \(k\) школьников, \(i\)-й школьник живет в доме, который находится на пересечении \(x_i\)-й строки и \(y_i\)-го столбца. Также у каждого школьника есть степень его агрессивности \(w_i\). Так как город оказался очень большим, Миша решил территориально ограничить действия своего сериала некоторым принадлежащим таблице квадратом \(s\), стороны которого параллельны осям координат и имеют длину от \(1\) до \(\min(n, m)\) клеток.
По сюжету главный герой приедет в город и сразу же попадет в квадрат \(s\). Обладая уникальной степенью агрессивности \(0\) он сможет проявить свои лидерские качества и собрать команду из спокойных, умеренных и агрессивных школьников.
Чтобы собранная команда была разносторонней, но сплоченной, агрессивности всех школьников в ней должны быть попарно различны и должны образовывать единый отрезок подряд идущих целых чисел. То есть, если внутри квадрата \(s\) найдутся школьники со степенями агрессивности \(l, l+1, \ldots, -1, 1, \ldots, r-1, r\), где \(l \le 0 \le r\), то главный герой сможет собрать команду из \(r-l+1\) человека (сам он тоже входит в эту команду).
Обратите внимание , брать в команду всех школьников из квадрата \(s\) не обязательно.
Миша считает, что в команде главного героя должно быть хотя бы \(t\) человек. Поэтому его интересует, сколько существует квадратов в таблице, попав в которые, главный герой сможет набрать команду как минимум из \(t\) человек. Помогите Мише это посчитать.
Первая строка содержит четыре целых числа \(n\), \(m\), \(k\) и \(t\) (\(1 \le n, m \le 40\,000\), \(1 \le n \cdot m \le 40\,000\), \(1 \le k \le 10^6\), \(1 \le t \le k + 1\)) — количество строк в таблице, количество столбцов, количество школьников, которые живут в городе и необходимый размер команды соответственно.
Каждая из \(k\) следующих строк содержит по три целых числа \(x_i\), \(y_i\) и \(w_i\) (\(1 \le x_i \le n\), \(1 \le y_i \le m\), \(1 \le \lvert w_i \rvert \le 10^9\)) — номер строки и номер столбца, на пересечении которых живет \(i\)-й школьник, а так же степень его агрессивности.
Выведите одно целое число — количество способов выбрать квадрат \(s\) таким образом, чтобы главный герой смог набрать команду, состоящую, хотя бы из \(t\) человек.
-
В первом тестовом примере главный герой ни в каком выбранном квадрате \(s\) не сможет набрать команду, состоящую из более чем одного человека.
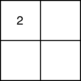 Иллюстрация к первому тестовому примеру.
Иллюстрация к первому тестовому примеру.
-
Во втором тестовом примере можно выбрать квадрат \(s\) двумя способами, изображенными ниже, в одном из них главный герой сможет набраться команду из школьников с степенями агрессивности \([0, 1]\), а в другом — \([0, 1, 2]\). Обратите внимание на то, что вне зависимости от выбранного квадрата главный герой со степенью агрессивности \(0\) всегда будет входить в команду.
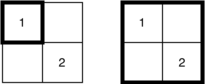 Иллюстрация ко второму тестовому примеру.
Иллюстрация ко второму тестовому примеру.
-
В третьем тестовом примере можно выбрать квадрат \(s\) четырьмя способами, изображенными ниже, в них главный герой сможет набраться команды со следующими степенями агрессивности школьников, соответственно: \([-1,0,1]\), \([0,1]\), \([0,1]\), \([-1, 0, 1]\).
 Иллюстрация к третьему тестовому примеру.
Иллюстрация к третьему тестовому примеру.
2 2 1 2 1 1 2
0
2 2 2 2 1 1 1 2 2 2
2
2 2 4 2 1 1 1 1 1 -1 1 2 1 2 2 1
4