Задача №115161. Башенки
Недавно в самом центре Флатляндии построили \(n\) невероятно красивых башен, \(i\)-я из которых находится в точке \(x_i\) и имеет высоту \(y_i\), а так же очень высокий отель в точке \(0\). В отеле \(q\) номеров и \(j\)-й из них находится на высоте \(h_j\).
Хозяин отеля ещё не определился с ценами номеров. Он убежден, что чем больше башен можно увидеть из номера, тем больше за него готовы платить, а потому поручил вам для каждого номера посчитать, сколько башен можно увидеть из него.
В этой задаче можно считать, что башни — это отрезки на плоскости, с координатами концов \((x_i, 0)\) и (\(x_i, y_i\)) соответственно. Номер в отеле — это точка с координатами \((0, h_j)\).
Башню \(i\) видно из номера отеля \(j\), если на отрезке \(\{(x_i, 0)\), \((x_i, y_i)\}\) есть точка \((a, b)\), такая что отрезок \(\{(0, h_j)\), \((a, b)\}\) не пересекается с отрезками других башен. Иными словами — на отрезке от отеля до какой-то точки башни ничего нет.
Обратите внимание: отрезки пересекаются, если имеют хотя бы одну общую точку, в том числе если их общая точка — конец какого-то из отрезков.
В первой строке входных данных находится одно целое число \(n\) (\(1 \le n \le 200\,000\)) — количество построенных башен.
В следующих \(n\) строках даны описания башен:
В \(i\)-й из них находятся два целых числа \(x_i\) и \(y_i\) \((1 \le x_i, y_i \le 10^9, x_i \neq x_j\) при \(i \neq j)\) — позиция и высота \(i\)-й башни соответственно.
В следующей строке дано одно целое число \(q\) \((1 \le q \le 200\,000)\) — количество номеров в отеле.
В следующих \(q\) строках даны описания комнат в отеле:
В \(j\)-й из них находится единственное целое число \(h_j\) \((1 \le h_j \le 10^9)\) — высота \(j\)-го номера в отеле.
Выведите \(q\) чисел. Для каждой комнаты в отеле — количество башен, которые видно из неё.
В тестовом примере 1 всего 4 запроса, вот иллюстрация каждого:
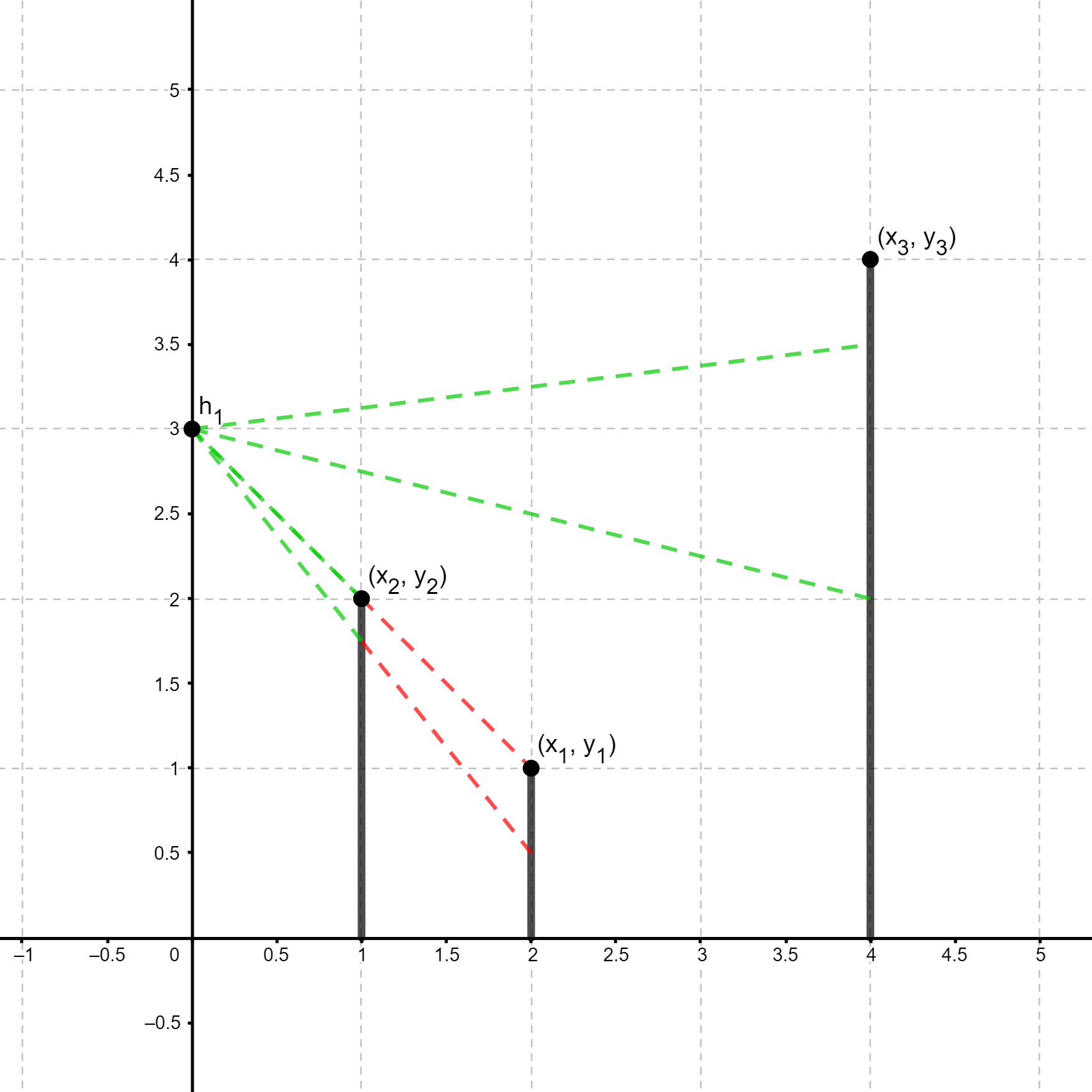
|
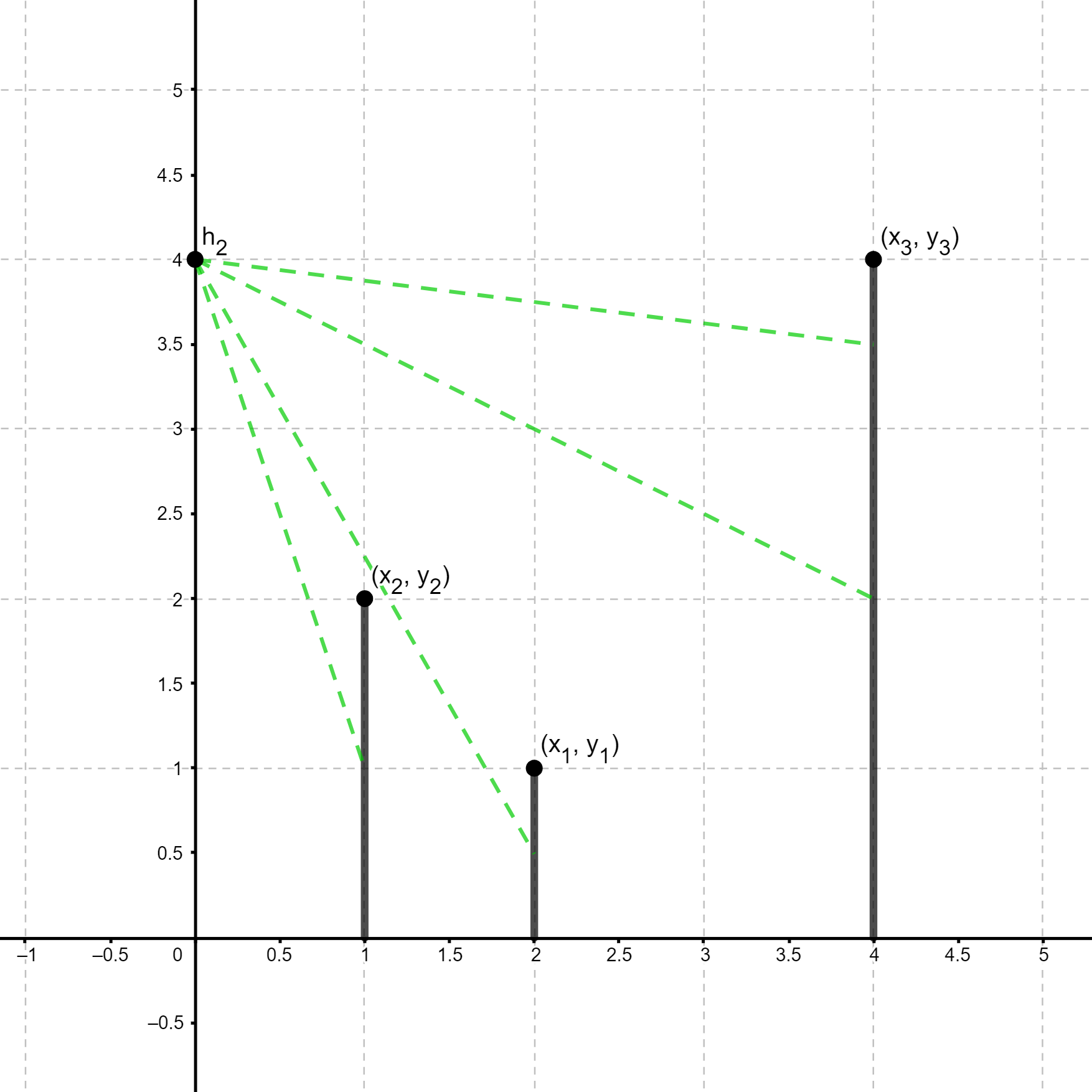
|
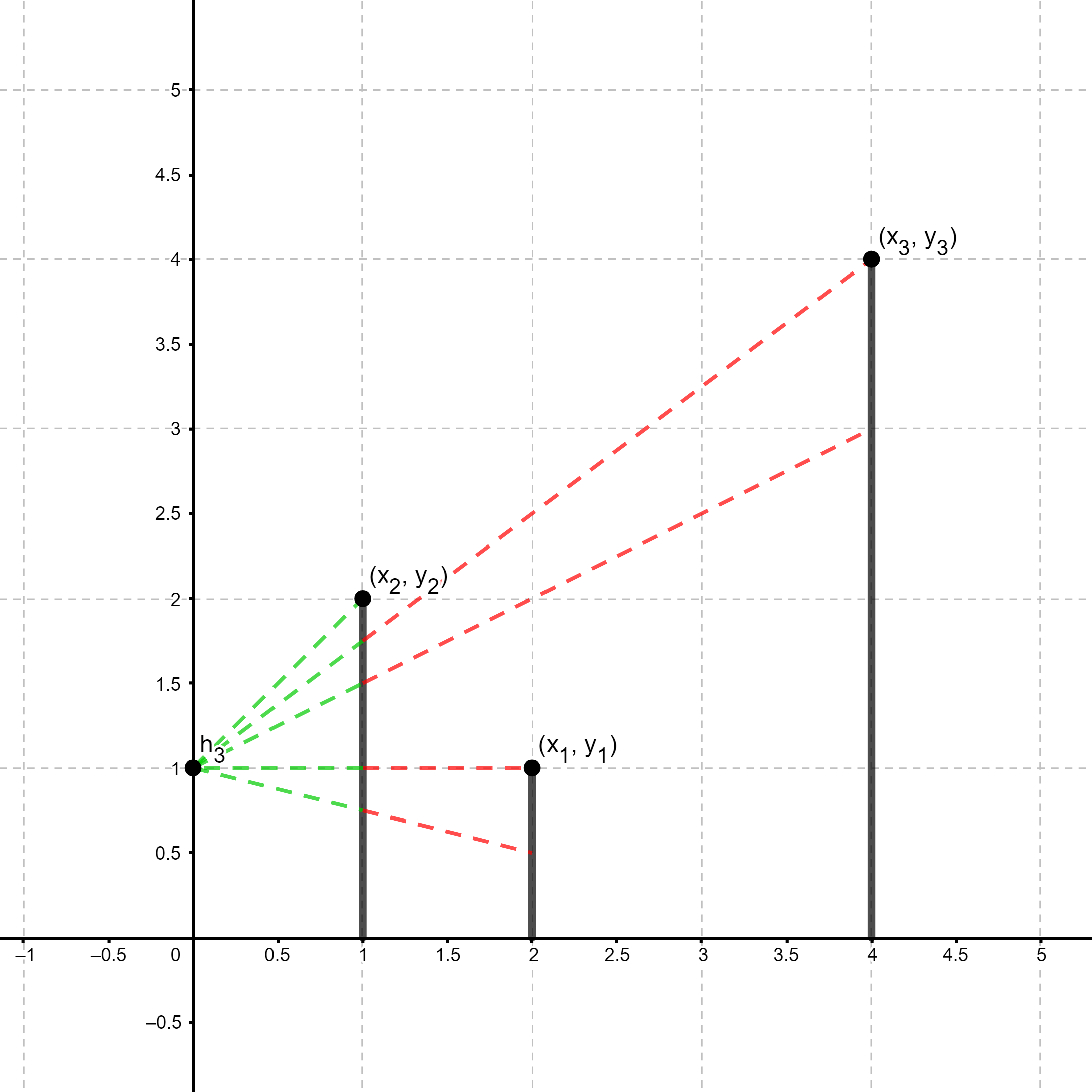
|
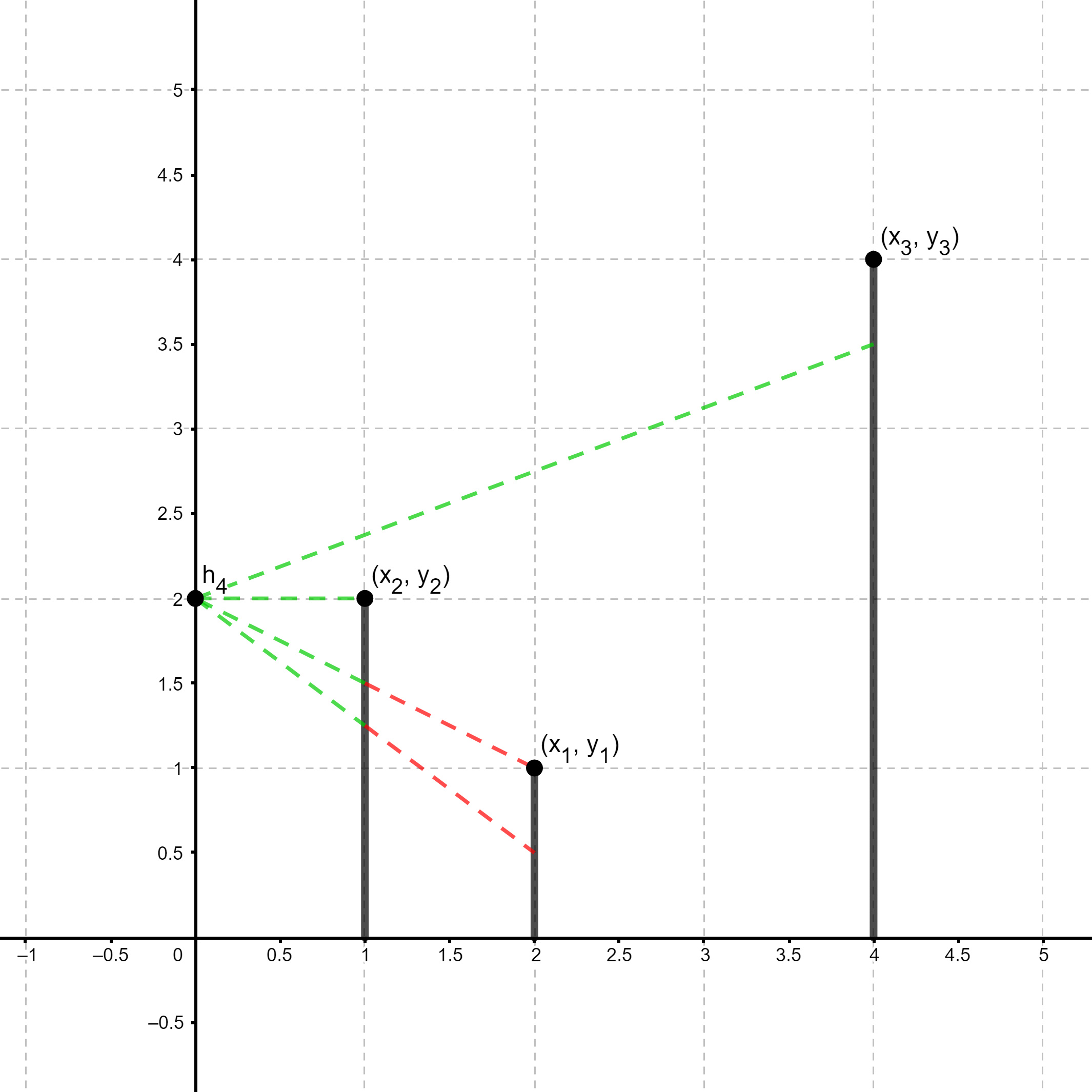
|
3 2 1 1 2 4 4 4 3 4 1 2
2 3 1 2
4 5 4 8 3 10 7 4 4 4 4 1 8 5
2 1 4 3