Открытая олимпиада школьников по программированию

Задача №115183. Задача для разминки ног

Однажды мальчик Кирилл долго и упорно пытался решить задачу с говорящим названием «Задача для разминки рук». Получилось ли у него решить задачу мы не знаем, однако, в процессе размышлений Кирилл придумал новую задачу, которую вам и предстоит решить. У Кирилла получилось следующее условие задачи:

В стране $X$ есть $n$ городов, соединённых $m$ дорогами. Множество дорог обладает двумя интересными свойствами. Во-первых, все дороги односторонние. Во-вторых, даже если бы дороги были двусторонними, для любой пары городов существовало бы не более одного простого пути между ними. Нетрудно заметить, что без ориентации граф на данных $n$ городах в качестве вершин и $m$ дорогах в качестве рёбер является лесом (то есть в каждой компоненте связности число ребер на единицу меньше числа вершин).

Функцию $cost(u, v)$ определим следующим образом: если путь из $u$ в $v$ существует, то она равна количеству дорог на этом пути, а если пути нет, то она равна $0$.

Красотой карты страны назовём величину $\sum\limits_{u=1}^{n}{\sum\limits_{v=1}^{n}{cost(u, v)}}$, то есть сумму величин $cost$ для всех пар городов.

Правительство страны $X$ очень любит считать различные статистики. В этот раз было решено посчитать красоту текущей карты страны, а так же обработать $q$ изменений карты страны, после каждого изменения подсчитывая её красоту .

Изменения бывают $4$ типов:

Добавить дорогу из города $u$ в город $v$.
Удалить дорогу между городами $u$ и $v$.
Изменить ориентацию дороги между городами $u$ и $v$ на противоположную.
Ориентировать все дороги на пути из $u$ в $v$ по направлению из $u$ в $v$. Гарантируется, что это возможно, то есть существует путь из города $u$ в город $v$ по дорогам, если игнорировать их ориентацию.

Гарантируется, что после каждого изменения множество городов и дорог продолжает образовывать лес.

Обратите внимание на то, что в данной задаче запросы меняют карту страны и зависят от предыдущих.

Входные данные

Первая строка содержит одно целое число $g$ ($0 \le g \le 10$) — номер группы тестов.

Вторая строка содержит три целых числа $n$, $m$ и $q$ ($2 \le n \le 400\,000$, $0 \le m < n$, $1 \le q \le 400\,000$) — количество городов, дорог и изменений соответственно.

Каждая из следующих $m$ строк содержит по два целых числа $u$ и $v$ ($1 \le u, v \le n$) — дороги на изначальной карте ориентированные из $u$ в $v$.

Каждая из следующих $q$ строк содержит по три целых числа $t$, $u$ и $v$ ($1 \le t \le 4$, $1 \le u, v \le n$) — тип запроса и пару вершин, задающую его.

Выходные данные

В первой строке выведите изначальную красоту карты страны.

В следующих $q$ строках выведите по одному числу — значения красоты карты страны после каждого изменения.

Примечание

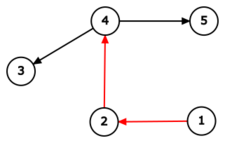
В тестовом примере до всех изменений граф выглядит так:

$\text{[math]}$

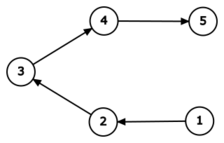
В этом случае, например, $cost(1, 2) = cost(2, 3) = cost(3, 4) = cost(4, 5) = 1$, так как между этими парами городов есть прямая дорога. Аналогично $cost(1, 3) = cost(2, 4) = cost(3, 5) = 2$, так как второй город в каждой паре достижим только за две дороги от первого. Так же, например, $cost(2, 1) = cost(4, 1) = cost(5, 3) = 0$, так как второй город в паре не достижим от первого. Суммируя эти величины по всем парам городов, получим $20$.

После этого надо изменить направление дороги между городами $3$ и $4$. Так как до этого она шла от города $3$ в город $4$, теперь она должна идти от города $4$ в город $3$. После этого ответ на задачу равен $6$, а граф имеет следующий вид:

$\text{[math]}$

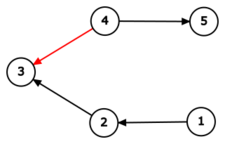
Далее дорога между городами $2$ и $3$ удаляется. После этого ответ на задачу равен $3$, а граф имеет следующий вид:

$\text{[math]}$

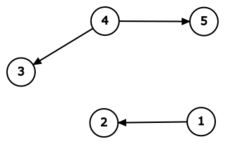
После этого добавляется дорога из города $4$ в город $2$. После этого ответ на задачу равен $4$, а граф имеет следующий вид:

$\text{[math]}$

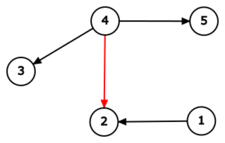
После этого, все дороги между городами $1$ и $4$ ориентируются по направлению из города $1$ в город $4$. После этого ответ на задачу равен $16$, а граф имеет следующий вид:

$\text{[math]}$

Система оценки

Тесты к этой задаче состоят из десяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

		Доп. ограничения
Группа	Баллы	$n$, $m$, $q$	Типы изменений	Необх. группы	Комментарий
0	0	–	–	–	Тесты из условия.
1	10	$n, m, q \le 100$	–	0
2	8	$n, m, q \le 5000$	–	0, 1
3	11	$n, m, q \le 100\,000$	1	–
4	7	$n, m, q \le 100\,000$	1, 2	3
5	13	$n, m, q \le 100\,000$	3	–
6	9	$n, m, q \le 100\,000$	3, 4	5
7	12	$n, m, q \le 100\,000$	–	–	$\|u - v\| = 1$ всегда, кроме запросов $4$ типа.
8	18	$n, m, q \le 100\,000$	–	0 – 7
9	6	$n, m, q \le 200\,000$	–	0 – 8	Offline-проверка.
10	6	–	–	0 – 9	Offline-проверка.

Примеры

Входные данные

Выходные данные

Сдать: для сдачи задач необходимо войти в систему